Key Concept
- Natural Numbers :All Non-negative counting numbers excluding zero are known as natural numbers.i.e. 5, 6, 7, 8, ……….
- Whole numbers : All non-negative counting numbers including zero are known as whole numbers.i.e. 0, 1, 2, 3, 4, 5,…………….
- Integers:All negative and non-negative numbers including zero altogether known as integers.i.e. ………. – 3, – 2, – 1, 0, 1, 2, 3, 4,…………..
- Even Numbers: A natural number is said to be even if it is multiple of 2 or it is divisible by 2.i.e. : 2, 4, 6, 8, 10, 12 ……. are examples of even numbers.
- Odd Numbers: A natural number is said to be odd, if it is not even or if it is not divisible by 2. i.e.1, 3, 5, 7, 9, ………. are examples of odd natural numbers.
- Consecutive Numbers: A series of natural numbers each differing by one is called consecutive numbers. i.e. 50, 51, 52, 53 are consecutive numbers.
- Prime Number: A natural number is said to be prime if it has only two different (distinct) factors namely one and itself. We say 4 and 9 are not prime whereas 2, 3, 5, 7, 11 are prime numbers.
- 1 is not a prime number
- The only even prime number is 2.
- The smallest prime number is 2.
- All prime numbers are odd except 2.
- Twin-prime: A pair of prime numbers is said to be twin-prime if they differ by 2. For example (3, 5), (11, 13), (17, 19), (29, 31), (29, 31), (41, 43), (71, 73) are all twin-prime.
- Composite Number: A natural number is said to be composite if it has at least three different factors. 4, 6, 12, are all composite numbers.
- 1 is not a composite number.
- 4 is the smallest composite number.
- 1 is neither prime nor composite.
- Algorithm: An algorithm gives us some definite steps to solve a particular type of problem in a well-defined manner.
- Lemma: A lemma is a statement which is already proved and is used for proving other statements.
- Euclid’s Division Algorithm :This is the technique to calculate the HCF (Highest common factor) of given two positive integers m and n,
- To calculate the HCF of two positive integers’ m and n with m > n, the following steps are followed:
- Step 1: Apply Euclid’s division lemma to find q and r where m = nq + r, 0 ≤ r < n.
- Step 2: If the remainder i.e. r = 0, then the HCF will be ‘n’ but if r ≠ 0 then we have to apply Euclid’s division lemma to n and r.
- Step 3: Continue with this process until we get the remainder as zero. Now the divisor at this stage will be HCF(m, n). Also, HCF (m, n) = HCF (n, r), where HCF (m, n) means HCF of m and n.
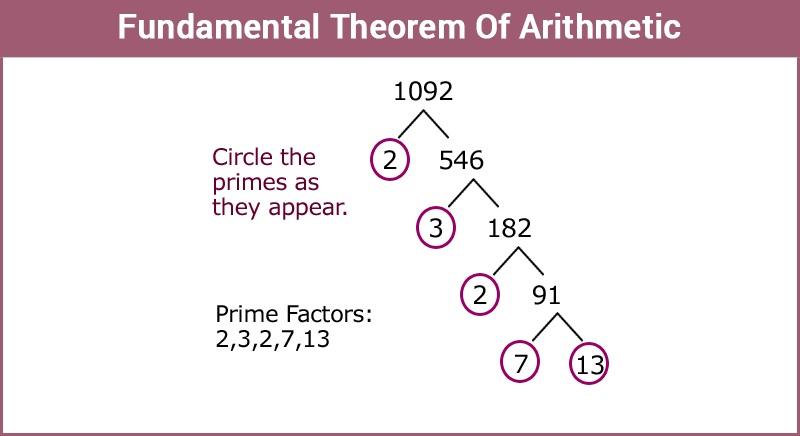
- The Fundamental Theorem of Arithmetic
We can factorize each composite number as a product of some prime numbers and of course, this prime factorization of a natural number is unique as the order of the prime factors doesn’t matter. - Theorem 1.1 (Fundamental Theorem of Arithmetic) : Every composite number can be expressed (factorised) as a product of primes, and this factorisation.
- HCF of given numbers is the highest common factor among all which is also known as GCD i.e. greatest common divisor.
- LCM of given numbers is their least common multiple.
- If we have two positive integers ‘m’ and ‘n’ then the property of their HCF and LCM will be:HCF (m, n) × LCM (m, n) = m × n.
- Rational Numbers:Rational numbers can be written in decimal form also which could be either terminating or non-terminating. E.g. 5/2 = 2.5 (terminating) and
 (non-terminating).
(non-terminating). - Irrational Numbers: The number ‘s’ is called irrational if it cannot be written in the form of p/q.
Questions & Answers
Q.1: Express each number as a product of its prime factors: (i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429
Solution:
Let's prime factorize the given numbers by the prime factorization method and then multiply the obtained prime numbers to get the product of the prime numbers.
(i) 140 = Prime factorization of 140 = 2 × 2 × 5 × 7 = 2² × 5 × 7
(ii) 156 = Prime factorization of 156 = 2 × 2 × 3 × 13 = 2² × 3 × 13
(iii) 3825 = Prime factorization of 3825 = 3 × 3 × 5 × 5 × 17 = = 3² × 5² × 17
(iv) 5005 = Prime factorization of 5005 = 5 × 7 × 11 × 13 =
(v) 7429 = Prime factorization of 7429 = 17 × 19 × 23
Q.2: Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers. (i) 26 and 91 (ii) 510 and 92 (iii) 336 and 54
Solution: LCM × HCF = Product of the two numbers.
- To find the LCM and HCF of the given pairs of the integers, first, find the prime factors of the given pairs of numbers.
- Then, find the product of the smallest power of each common factor in the numbers. This will be the LCM.
- Then, find the product of the greatest power of each prime factor in the number. This would be the HCF.
- Now, we have to verify LCM × HCF = product of the two numbers.
(i) 26 and 91
Prime factors of 26 = 2 × 13
Prime factors of 91 = 7 × 13
HCF of 26 and 91 = 13
LCM of 26 and 91 = 2 × 7 × 13 = 14 × 13 = 182
Product of these two numbers = 26 × 91 = 2366
LCM × HCF = 182 × 13 = 2366
Thus, the product of two numbers = LCM × HCF
(ii) 510 and 92
Prime factors of 510 = 2 × 3 × 5 × 17
Prime factors of 92 = 2 × 2 × 23
HCF of the two numbers = 2
LCM of the two numbers = 2 × 2 × 3 × 5 × 17 × 23 = 23460
Product of these two numbers = 510 × 92 = 46920
LCM x HCF = 2 × 23460 = 46920
Thus, the product of two numbers = LCM × HCF
(iii) 336 and 54
Prime factors of 336 = 2 × 2 × 2 × 2 × 3 × 7
Prime factors of 54 = 2 × 3 × 3 × 3
HCF of the two numbers = 6
LCM of the two numbers = 2 × 2 × 2 × 2 × 3 × 3 × 3 × 7 = 24 × 33 × 7 = 3024
Product of these two numbers = 336 × 54 = 18144
LCM x HCF = 3024 × 6 = 18144
Thus, the product of two numbers = LCM × HCF
Q.3: Find the LCM and HCF of the following integers by applying the prime factorization method: (1) 12, 15 and 21 (2) 17, 23 and 29 (3) 8, 9 and 25
- The largest possible number which divides the given numbers exactly without any remainder is called the highest common factor of the given numbers.
- Least Common Multiple of a and b is the smallest number that divides a and b exactly
Answer: (1) LCM(12, 15, 21) = 420, HCF(12, 15, 21) = 3 (2) LCM(17, 23, 29) = 11339, HCF(17, 23, 29) = 1 (3) LCM(8, 9, 25) = 1800, HCF(8, 9, 25) = 1.
(1) 12, 15 and 21
Prime factorization of 12: 2 × 2 × 3 = 22 × 3
Prime factorization of 15: 3 × 5
Prime factorization of 21: 3 × 7
LCM of 12, 15, and 21 is given as:
LCM(12, 15, 21) = 22 × 3 × 5 × 7 = 4 × 3 × 5 × 7 = 420
HCF of 12, 15, and 21 is given as:
Common factors of the three numbers are: 3
HCF(12, 15, 21) = 3
(2)17, 23 and 29
Prime factorization of 17: 17
Prime factorization of 23: 23
Prime factorization of 29: 29
LCM of 17, 23, and 29 is given as:
LCM(17, 23, 29) = 17 × 23 × 29 = 11339
HCF of 17, 23, and 29 is given as:
Since there's not any common factor
Hence, HCF(17, 23, 29) = 1
(3) 8, 9 and 25
Prime factorization of 8: 2 × 2 × 2 = 23
Prime factorization of 9: 3 × 3 = 32
Prime factorization of 25: 5 × 5 = 52
LCM of 8, 9, and 25 is given as:
LCM(8, 9, 25) = 23 × 32 × 52 = 8 × 9 × 25 =1800
HCF of 8, 9, and 25 is given as:
Since there's no common factor
Hence, HCF(8, 9, 25) = 1
Thus, (1) LCM(12, 15, 21) = 420, HCF(12, 15, 21) = 3 (2) LCM(17, 23, 29) = 11339, HCF(17, 23, 29) = 1 (3) LCM(8, 9, 25) = 1800, HCF(8, 9, 25) = 1.
Q.4: Given that HCF (306, 657) = 9, find LCM (306, 657)
Solution: We know that LCM × HCF = product of two given integers
Given, HCF (306, 657) = 9
We have to find, LCM (306, 657)
We have the given numbers 306 and 657. Hence, we can find the product of 306 and 657. The HCF of these two numbers is 9. Substitute these values in the above formula and find the value of the unknown i.e. LCM.
LCM × 9 = 306 × 657
LCM = (306 × 657) / 9
LCM = 34 × 657
LCM = 22338
Q.5: Question: Check whether 6n can end with the digit 0 for any natural number n.
If any digit has the last digit 0 that means it divisible by 2 or/and 5.
So value of 6n should be divisible by 2 and 5.
Q.6: Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
The numbers 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers since on simplification the numbers have (2,3,13 and 1) and (5,1009 and 1) as their factors respectively.
Q.7: There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?

Given:
- Sonia takes 18 minutes to drive one round of the field.
- Ravi takes 12 minutes for the same.
- They both start at the same point and at the same time and go in the same direction.
Time taken by Sonia is more than Ravi to complete one round. Now, we have to find after how many minutes will they meet again at the same point. For this, there will be a number that is divisible by both 18 and 12, and that will be the time when both meet again at the starting point. To find this we have to take LCM of both numbers.
Let's find LCM of 18 and 12 by prime factorization method.
18 = 2 × 3 × 3
12 = 2 × 2 × 3
LCM of 12 and 18 = 2 × 2 × 3 × 3 = 36
Therefore, Ravi and Sonia will meet together at the starting point after 36 minutes.

