Concepts
- Trigonometry: It shows the relationship between the sides and the angles of the triangle. Generally, it is used in the case of a right angle triangle.
- Trigonometric Ratios : In a right angle triangle, the ratio of its side and the acute angles is the trigonometric ratios of the angles. In this right angle triangle ∠B = 90°. If we take ∠A as acute angle then

- sin θ = Perpendicular/Hypotenuse = p/h
- cos θ = Base/Hypotenuse = b/h
- tan θ = Perpendicular/Base = p/b
The value of the other three functions: cot, sec, and cosec depend on tan, cos, and sin respectively as given below.
- cot θ = 1/tan θ = Base/Perpendicualr = b/p
- sec θ = 1/cos θ = Hypotenuse/Base = h/b
- cosec θ = 1/sin θ = Hypotenuse/Perpendicular = h/p
Note : For ∠A — Perpendicular is BC and base is AB. For ∠C, Perpendicular is AB Base is BC ( Very Very Important )
- Trigonometric ratios with respect to ∠A
| Ratio | Formula | Short form | Value |
| sin A | P/H | BC/AC | |
| cos A | B/H | AB/AC | |
| tan A | P/B | BC/AB | |
| cosec A | H/P | AC/BC | |
| sec A | H/B | AC/AB | |
| cot A | B/P | AB/BC |
Remarks:
- If we take ∠C as acute angle then BC will be base and AB will be perpendicular. Hypotenuse remains the same i.e. AC. So the ratios will be according to that only.
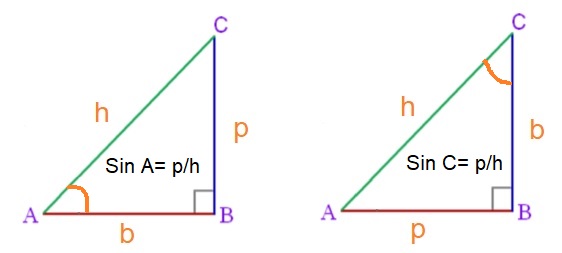
Sin A = Perpendicular/Hypotenuse = p/h = BC / AC
Sin C = Perpendicular/Hypotenuse = p/h = AB / AC ( V. Imp Concept )
- If the angle is same then the value of the trigonometric ratios of the angles remain the same whether the length of the side increases or decreases.
- In a right angle triangle, the hypotenuse is the longest side so sin A or cos A will always be less than or equal to 1 and the value of sec A or cosec A will always be greater than or equal to 1.
Reciprocal Relation between Trigonometric Ratios
Cosec A, sec A, and cot A are the reciprocals of sin A, cos A, and tan A respectively.

Relation:
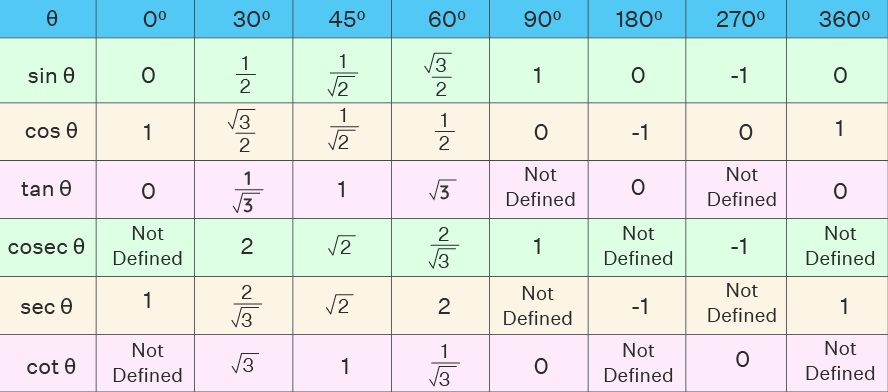
Trigonometric Ratios of Some Specific Angles
Trigonometric Ratios of Complementary Angles
If the sum of two angles is 90° then, it is called Complementary Angles. In a right-angled triangle, one angle is 90 °, so the sum of the other two angles is also 90° or they are complementary angles.so the trigonometric ratios of the complementary angles will be :
sin (90° – A) = cos A,
cos (90° – A) = sin A,
tan (90° – A) = cot A,
cot (90° – A) = tan A,
sec (90° – A) = cosec A,
cosec (90° – A) = sec A
Supplementary Angles
Supplementary angles are formed when the total of two angles equals 180 degrees. In other words, supplementary angles are formed when two angles are added together to make a straight angle.
The two angles constitute a linear angle, with one angle equal to x and the other equal to 180 – x. The fact that the angles are linear demonstrates that their qualities do not change. Consider the following trigonometric ratios:
- Sin (180 – A) = Sin A
- Cos (180 – A) = – Cos A (quadrant is changed)
- Tan (180 – A) = – Tan A
Trigonometric Identities (Pythagoras Identity)
An equation is said to be a trigonometric identity if it contains trigonometric ratios of an angle and satisfies it for all values of the given trigonometric ratios.

In ∆PQR, right angled at Q, we can say that
PQ2 + QR2 = PR2
Divide each term by PR2, we get

(sin R)2 + (cos R)2 = 1
sin2 R + cos2 R =1
Likewise other trigonometric identities can also be proved. So the identities are-
- sin2 θ + cos2 θ = 1
- 1 + tan2 θ = sec2 θ
- cot2 θ + 1 = cosec2 θ
The three important trigonometric identities are:
- sin²θ + cos²θ = 1 or sin²θ = 1- cos²θ
- tan²θ + 1 = sec²θ or sec²θ - tan²θ = 1
- cot²θ + 1 = cosec²θ or cosec²θ - cot²θ = 1
How to solve the problems related to trigonometric ratios and identities?
Prove that

L.H.S

(by reciprocal identity and quotient identity)

(by simplifying the denominator and by Pythagoras identity)

Hence, L.H.S = R.H.S


