Concepts
Types of Triangles
1. There are three types of Triangles on the basis of the length of the sides.

2. There are three types of Triangles on the basis of angles.

Angle Bisector Theorem
Angle bisector theorem states that an angle bisector divides the opposite side into two line segments that are proportional to the other two sides.
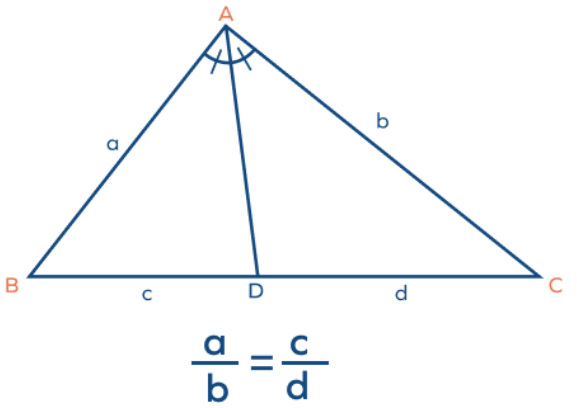
Here, in ΔABC, the line AD is the angle bisector of ∠A.
AD bisects the side BC in two parts, c and d.
a and b are the lengths of the other two sides.
By the angle bisector theorem, we have
BD/ DC = AB / AC
Or
BD:DC = AB:AC
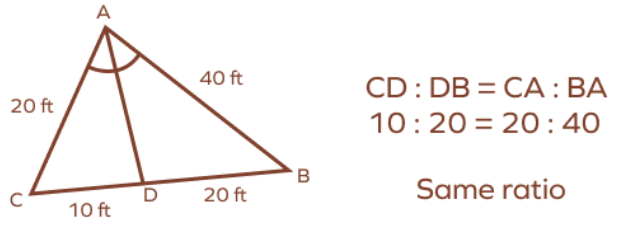
Example:
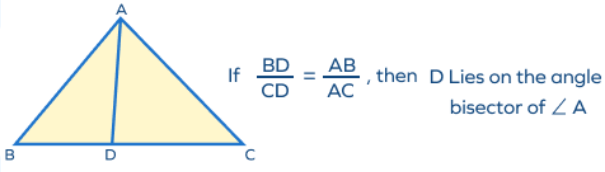
Converse of Angle Bisector Theorem
The converse of the angle bisector theorem states that if the interior point of an angle of a triangle is equidistant from the two sides (arms) of a triangle, then that point lies on the angle bisector of the angle.
Centers of the Triangle
There are four different centers of the Triangle
1. Centroid of a Triangle
The point of intersection of the medians of the three sides of the Triangle is the centroid of that Triangle. It will always inside the Triangle.

2. Incenter of a Triangle
The point of intersection of the angle bisectors of the three angles of the Triangle is called the incenter of that Triangle. It is the point from where the circle is inscribed in the Triangle. The radius is find by drawing the perpendicular from the incenter to any of the side of the Triangle.

3. Circumcenter of the Triangle
The point of intersection of the perpendicular bisectors of the three vertices of the Triangle is called the circumcenter of that Triangle. It is not always inside the Triangle. It could be outside the Triangle for obtuse Triangle and fall at the midpoint of the hypotenuse of the right angled Triangle.
4. Orthocenter
The point of intersection of the altitudes of the Triangle is the orthocenter of that Triangle. Like circumcenter , it also falls outside the Triangle in case of obtuse Triangle and it falls at the vertex of the Triangle in case of right angle Triangle.

Congruent vs. Similar figures
Congruent |
Similar |
|
Angles |
Corresponding angles are same. | Corresponding angles are same. |
Sides |
Corresponding sides are same. | Corresponding sides are proportional. |
Example |
 |
 |
Explanation |
Both the square have the same angles and same side. | Both the squares have same angles but not the same sides. |
Symbols |
 |
 |
The above explanation shows that if two figures are congruent then they will be similar also but it is not necessary that if two figures are similar then they will be congruent also.
Similarity of Triangles
In the Triangles also we will use the same condition that the two Triangles will be similar if-
- The corresponding angles of the two Triangles are same and
- The corresponding sides of the two Triangles are in same proportion.

The above two Triangles ∆ABC and ∆DEF are similar as-

If the corresponding angles of the two Triangles are same then they are called equiangular Triangles.
Basic Proportionality Theorem (Thales Theorem)
According to Thales theorem, if in a given Triangle a line is drawn parallel to any of the sides of the Triangle so that the other two sides intersect at some distinct point then it divides the two sides in the same ratio.
In ∆KMN, if PQ║MN and intersects KM at P and KN at Q, then,

Converse of Basic Proportionality Theorem
It is the opposite of basic proportionality theorem, which says that if in a given Triangle a straight line divides the two sides of the Triangle in the same ratio then that straight line is parallel to the third side of the Triangle.

Criteria for the similarity of Triangles
Basically, there are three criteria to find the similarity of two Triangles.
1. AAA(angle-Angle-Angle) criteria of similarity
If in two given Triangles all the corresponding angles are equal then their corresponding sides will also be in proportion.
This shows that all the corresponding angles in the ∆ABC and ∆PQR are same so their corresponding sides are in proportion, that why the two Triangles similar.
Hence, ∆ABC ~ ∆PQR
Remark: If the two corresponding angles of the two Triangles are equal then according to the sum of angles of Triangle, the third angle will also be equal. So two Triangles will be similar if their two angles are equal with the two angles of another Triangle.This is known as AA (Angle-Angle) criteria.
2. SSS(Side-Side-Side) criteria of similarity
If in the two Triangles, all the sides of one Triangle are in same ratio with the corresponding sides of the other Triangle, then their corresponding angles will be equal. Hence the two Triangles are similar.
-criteria-of-similarity.png)
In ∆ABC and ∆DEF

Hence, ∆ABC ~ ∆DEF
Remark: The above two criterions shows that if any of the two criteria satisfies then the other implies itself. So we need not check for both the conditions to satisfy to find the similarity of the two Triangles. If all the angles are equal then all the sides will be in proportion itself and vice versa.
3. SAS(Side-Angle-Side) criteria of similarity
If in the two Triangles, two sides are in the same ratio with the two sides of the other Triangle and the angle including those sides is equal then these two Triangles will be similar.
In ∆ABC and ∆KLM

Hence, ∆ABC ~ ∆KLM
Areas of similar Triangles
If the two similar Triangles are given then the square of the ratio of their corresponding sides will be equal to the ratio of their area.

If ∆ABC ~ ∆PQR, then

Pythagoras Theorem (Baudhayan Theorem)
Pythagoras theorem says that in a right angle Triangle, the square of the hypotenuse i.e. the side opposite to the right angle is equal to the sum of the square of the other two sides of the Triangle.
If one angle is 90°, then a2 + b2 = c2
Example
In the given right angle Triangle, Find the hypotenuse.

Solution
AB and BC are the two sides of the right angle Triangle.
BC = 12 cm and AB = 5 cm
From Pythagoras Theorem, we have:
CA2 = AB2 + BC 2
= (5)2 + (12)2
= 25+144
So, AC2 = 169
AC = 13 cm
Converse of Pythagoras Theorem
In a Triangle, if the sum of the square of the two sides is equal to the square of the third side then the given Triangle is a right angle Triangle.
If a2 + b2 = c2 then one angle is 90°.
Similarity of two Triangles made in right angle Triangle
In a right angle Triangle, if we draw a perpendicular from the right angle to the hypotenuse of the Triangle, then both the new Triangles will be similar to the whole Triangle.

In the above right angle Triangle CP is the vertex on the hypotenuse, so
∆ACP ~ ∆ACB
∆PCB ~ ∆ACB
∆PCB ~ ∆ACP


