Concept
If two or more parts of a figure are identical after folding or flipping then it is said to be symmetry.
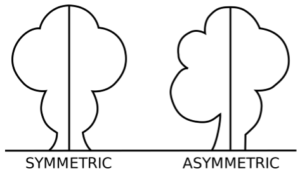
Symmetry: A shape is said to be symmetric if it can be divided into two more identical pieces.
Line of Symmetry: It is an imaginary line which divides the image into two equal halves. It could be horizontal, vertical or diagonal.
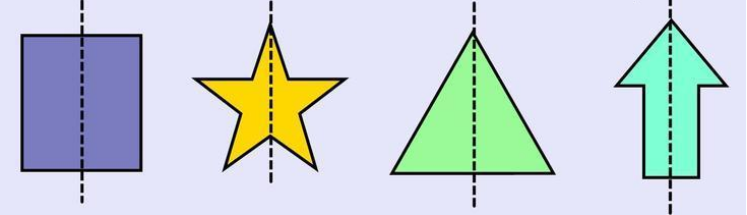
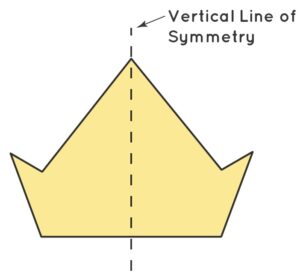
Vertical Line of Symmetry : A vertical line of symmetry is that line that runs down vertically, divides an image into two identical halves.
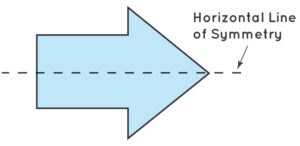
Horizontal Line of Symmetry: The horizontal line of symmetry divides a shape into identical halves, when split horizontally.
Diagonal Line of Symmetry: A diagonal line of symmetry divides a shape into identical halves when split across the diagonal corners.
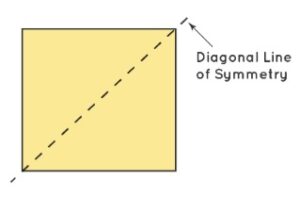
Rotational Symmetry :When an object is rotated in a particular direction, around a point, then it is known as rotational symmetry.

Rotational symmetry in regular shapes
Many 2D shapes have a rotational symmetry. If a shape is rotated around its centre and the shape returns to the original position without it “fitting into itself”, then the shape is described to have no rotational symmetry. Irregular shapes tend to have no rotational symmetry. Regular polygons have the same number of sides as their rotational symmetry.
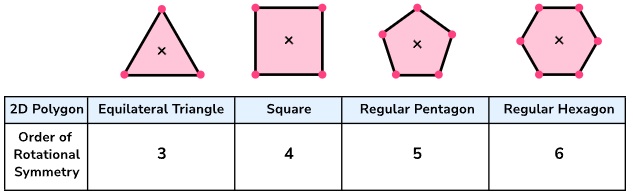
In the regular polygon, the number of lines of symmetry is the same as the number of its sides.
| Regular Polygon | Number of Sides | Line of Symmetry | Image |
| Equilateral Triangle | 3 | 3 |  |
| Square | 4 | 4 |  |
| Regular Pentagon | 5 | 5 |  |
| Regular Hexagon | 6 | 6 |  |
Reflection Symmetry
If we draw a dotted line which gives the mirror reflection of the other half of the image then it is reflection symmetry. It is the same as basic symmetry which tells us that if the dotted line divides the image into two equal halves then it is the reflective symmetry of the figure.

2. Rotational Symmetry
If we rotate the image at a centre point of the image at 360° then the number of times the image looks the same, shows the rotational symmetry of the image.
Rotational Symmetry
- If a figure rotates at a fixed point then that point is the centre of Rotation.
- It could rotate clockwise or anticlockwise.
- While rotation the measurement of the angle which we take is the angle of rotation. And a complete rotation is of 360°.
- If the angle of rotation is 180° then it is called Half Turn and if the angle of rotation is 90° then it is called a Quarter Turn.

This image looks symmetrical but there is no line of symmetry in it i.e. there is any such line which divides it into two equal halves. But if we rotate it at 90° about its centre then it will look exactly the same. This shows that it has Rotational Symmetry.
While rotating, there are four positions when the image looks exactly the same. So this windmill has a rotational symmetry of order 4 about its centre.
Example
What is the Rotational symmetry of the given figure?

Solution:
To find the rotational symmetry, we have to find
- The angle of rotation = 90°
- Direction = clockwise
- Order of rotation = 4
This shows that if the given figure rotates anticlockwise at 90° around its centre then it has rotational symmetry of order 4.
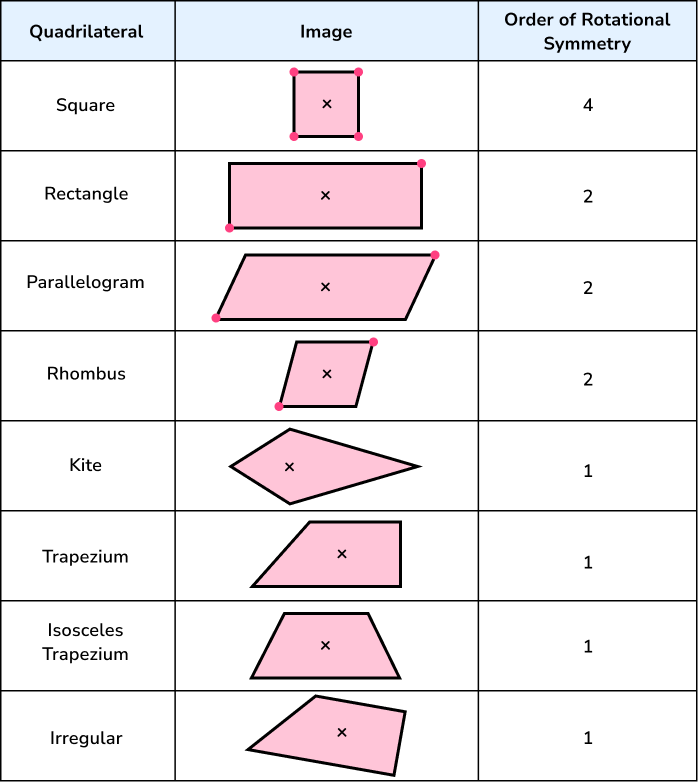
Let’s look at different shapes (specifically quadrilaterals) and their order of rotational symmetry.
Line Symmetry and Rotational Symmetry
Some shapes have only line symmetry and some shapes have only rotational symmetry but there are some shapes which have both types of symmetry.
Example
Find whether the given image has rotational symmetry or line symmetry or both.

Solution:
Rotational Symmetry
If we rotate the image clockwise at an angle of 360° around its centre then it will have rotational symmetry of order 1 or no symmetry as every image will look same if we rotate it at 360°.
This will not look the same at every 120° because of the colour of the balls at its edges.

Line Symmetry
This figure will have three line of symmetry. As there are three possible lines which can divide the image into two equal halves.

Example
Tell whether the figures below have line symmetry or rotational symmetry or both.

Solution:
- The first figure have 2 line of symmetry and rotational symmetry of order 2.
- The second figure has no line of symmetry but have rotational symmetry of order 3.
- The third figure has 1 line of symmetry but no rotational symmetry.
- The fourth figure has 1 line of symmetry but no rotational symmetry.

