Concepts
The square of a number is the number multiplied by itself. Example : 2 x 2 = 22 = 4
- Numbers Between n2 and (n+1)2 = 2n, where n is any natural number
- Remember that: (-) x (-) = (+)Therefore, square of (-n), (-n)2 = (-n) x (-n) = n2Where n is a number.
Examples:
- (-5)2 = (-5) x (-5) = 25
- (-7)2 = (-7) x (-7) = 49
Square Numbers 1 to 50
| 12 = 1 | 112 = 121 | 212 = 441 | 312 = 961 | 412 = 1681 |
| 22 = 4 | 122 = 144 | 222 = 484 | 322 = 1024 | 422 = 1764 |
| 32 = 9 | 132 = 169 | 232 = 529 | 332 = 1089 | 432 = 1849 |
| 42 = 16 | 142 = 196 | 242 = 576 | 342 = 1156 | 442 = 1936 |
| 52 = 25 | 152 = 225 | 252 = 625 | 352 = 1225 | 452 = 2025 |
| 62 = 36 | 162 = 256 | 262 = 676 | 362 = 1296 | 462 = 2116 |
| 72 = 49 | 172 = 289 | 272 = 729 | 372 = 1369 | 472 = 2209 |
| 82 = 64 | 182 = 324 | 282 = 784 | 382 = 1444 | 482 = 2304 |
| 92 = 81 | 192 = 361 | 292 = 841 | 392 = 1521 | 492 = 2401 |
| 102 = 100 | 202 = 400 | 302 = 900 |
Square root of any number is the value which when multiplied by itself gives the original number. It is denoted by the symbol, ‘√’. If the square root of n is a, then a multiplied by a is equal to n. It can be expressed as:
√n = a then a x a = n
This is the formula for square root.
Square Roots of Perfect Squares
The perfect squares are the one whose square root gives a whole number. For example, 4 is a perfect square because when we take the square root of 4, it is equal to 2, which is a whole number. Let us see some of the perfect squares and their square roots.
| Perfect Squares | Square Root (√) |
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
| 25 | 5 |
Square Root of Imperfect Squares
Finding the square root of perfect squares is easy but to find the root of imperfect squares is difficult. The root of the perfect square can be estimated using the prime factorisation method.
The square root of imperfect squares is usually fractions. For example, 2 is an imperfect square because 2 cannot be prime factorised and its square root gives a fractional value.
Examples are:
- √2 = 1.4142
- √3 = 1.7321
- √8 = 2.8284
Square Roots 1 to 50
| Number | Square Root | Number | Square Root | Number | Square root |
| √1 | 1 | √18 | 4.2426 | √35 | 5.9161 |
| √2 | 1.4142 | √19 | 4.3589 | √36 | 6 |
| √3 | 1.7321 | √20 | 4.4721 | √37 | 6.0828 |
| √4 | 2 | √21 | 4.5826 | √38 | 6.1644 |
| √5 | 2.2361 | √22 | 4.6904 | √39 | 6.2450 |
| √6 | 2.4495 | √23 | 4.7958 | √40 | 6.3246 |
| √7 | 2.6458 | √24 | 4.8990 | √41 | 6.4031 |
| √8 | 2.8284 | √25 | 5 | √42 | 6.4807 |
| √9 | 3 | √26 | 5.0990 | √43 | 6.5574 |
| √10 | 3.1623 | √27 | 5.1962 | √44 | 6.6332 |
| √11 | 3.3166 | √28 | 5.2915 | √45 | 6.7082 |
| √12 | 3.4641 | √29 | 5.3852 | √46 | 6.7823 |
| √13 | 3.6056 | √30 | 5.4772 | √47 | 6.8557 |
| √14 | 3.7417 | √31 | 5.5678 | √48 | 6.9282 |
| √15 | 3.8730 | √32 | 5.6569 | √49 | 7 |
| √16 | 4 | √33 | 5.7446 | √50 | 7.0711 |
| √17 | 4.1231 | √34 | 5.8310 |
How to find the square root?
To find the square root of a number we can use the prime factorisation method. For example, the square root of 900 is:
√900 = √(2 x 2 x 3 x 3 x 5 x 5 )
Taking out the numbers in pairs, we get;
√900 = 2 x 3 x 5 = 30
900 was a perfect square, but to find the root of an imperfect square, we have to use long division method.
Properties of Square Root.
- Numbers ending with 0, 1, 4, 5, 6, or 9 at units place are perfect squares.
- Numbers ending with 2, 3, 7, 8 are not perfect squares.
- The number of zeros at the end of a perfect square is always even.
-
The square of an even number is always an even number and square of an odd number is always an odd number.E.g.
- There are ‘2a’ non perfect square numbers between the square of two Consecutive natural numbers.
- Sum of first odd natural numbers = n2
- A number ending in an odd number of zeros is never a perfect square.
- Examples: 3530,55849000,384850003530,55849000,38485000 are not perfect squares. However, this does not mean that all numbers ending in an even number of zeros are always perfect squares. These may or may not be perfect squares.
- Examples: 500500 is not a perfect square. 400400 is a perfect square.
- Examples: 3530,55849000,384850003530,55849000,38485000 are not perfect squares. However, this does not mean that all numbers ending in an even number of zeros are always perfect squares. These may or may not be perfect squares.
- The square of even numbers is always even.
What are Pythagorean Triples?

The integer solutions to the Pythagorean Theorem, a2 + b2 = c2 are called Pythagorean Triples which contains three positive integers a, b, and c.
Example: (3, 4, 5)
By evaluating we get:
32 + 42 = 52
9+16 = 25
Hence, 3,4 and 5 are the Pythagorean triples.
You can say “triplets,” but “triples” are the favoured term. Let’s start this topic by an introduction of Pythagoras theorem.
Table
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
How to find Pythagorean triplets?
If a, b are two sides of the triangle and c is the hypotenuse, then, a, b, and c can be found out using the following formula-
Solution: Given, (16, 63, 65)
a = 16, b = 63, c = 65
Pythagorean triples formula used as,
c2 = a2 + b2
LHS: c2 = 652 = 4225
RHS: a2 + b2 = 162 + 632 = 256 + 3969 = 4225
LHS = RHS
So, (16, 63, 65) is a Pythagorean triples.
Write a Pythagorean triplet whose one member is 18
Solution: Let 2m = 18 , m = 9
Now, m2 – 1 = 92 – 1 =81 – 1 = 80
And, m2 + 1 = 92 + 1 = 81 + 1 = 82
So, the Pythagorean triple is 18, 80, 82
Questions & Answers
Let us find the square root of 180.
Step 1: Place a bar over every pair of digits of the number starting from the units' place (right-most side). We will have two pairs, i.e., 1 and 80
Step 2: We divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.
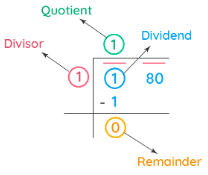
Step 3: Bring down the number under the next bar to the right of the remainder. Add the last digit of the quotient to the divisor. To the right of the obtained sum, find a suitable number which, together with the result of the sum, forms a new divisor for the new dividend that is carried down.

Step 4: The new number in the quotient will have the same number as selected in the divisor. The condition is the same — as being either less than or equal to the dividend.
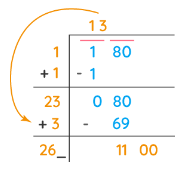
Step 5: Now, we will continue this process further using a decimal point and adding zeros in pairs to the remainder.
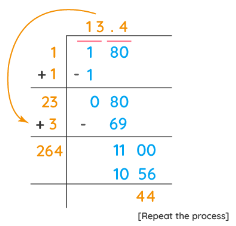
Step 6: The quotient thus obtained will be the square root of the number. Here, the square root of 180 is approximately equal to 13.4 and more digits after the decimal point can be obtained by repeating the same process as follows.

Example: Solve the equation √(2x + 3) = 10.
Solution:
Squaring on both sides of the equation would result in the cancellation of the square root on the left side.
2x + 3 = 102
2x + 3 = 100
2x = 97
x = 97/2 = 48.5
Square Root Table
The square root table consists of numbers and their square roots. It is useful to find the squares of numbers as well. Here is the list of square roots of perfect square numbers and some non-perfect square numbers from 1 to 10.
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
Find out the square root of 529 by the prime factorization method.
Solution:
Prime factorization of 529.

We can see that, 529 = 23×23 ⇒ √529= 23
∴ √529= 23.
Answer: 23
Find the square and square root of the following numbers.
a) Square root of 25 is ___
b) Square of 16 is ____
c) Square of 20 is ____
d) Square root of 400 is _____
Solution:
a) Square root of 25 is 5
5 × 5 = 25
√25 = 5
b) Square of 16 is = 16 × 16 = 256
c) Square of 20 is = 20 × 20 = 400
d) Square root of 400 is 20 as
20 × 20 = 400
√400 = 20.
Answer: a) 5 b) 256 c) 400 d) 20
Determine the square root of 60.
Solution:
To find: square root of 60
From prime factorization of 60, we get,
60 = 2 × 2 × 3 × 5
= (2)2 × 3 × 5
Using square root formula,
√60 = [(2)2 × 15 ]1/2
√60 = 2√15
Therefore, Square root of 60 = 2√15
Answer: 2√15

