Key Concepts
- Set: A set is defined as a well-defined collection of objects.
- Some standard sets in maths are:
- Set of natural numbers, ℕ = {1, 2, 3, ...}
- Set of whole numbers, W = {0, 1, 2, 3, ...}
- Set of integers, ℤ = {..., -3, -2, -1, 0, 1, 2, 3, ...}
- Set of rational numbers, ℚ = {p/q | q is an integer and q ≠ 0}
- Set of irrational numbers, ℚ' = {x | x is not rational}
- Set of real numbers, ℝ = ℚ ∪ ℚ'
- Elements of a Set :The items present in a set are called either elements or members of a set.
- Set A = {2, 4, 6, 8}, which is a finite set.
- In the above example, 2 ∈ A and 3 ∉ A. it means , 2 is the element of set A or 2 belongs to set A but 3 is not the element of A.
- Methods to represent a set:
- Description Method : by describing in words
- Set A = The set of all English alphabets
- Set B = The set of whole numbers
- Roster Method : Tabular form , separated by commas.
- A = {2, 4, 6, 8, 10}
- N = {1, 2,3, 4, 5,6, ....................}
- Set Builder Method : In set builder form, all the elements have a common property.
- S = {x/x has property P} or S = {x: x has property P}
- Let B = {3,6,9,12,15} , Thus the set builder form is B = { x: x = 3n , where n ∈ ℕ and n ≤ 5 }
- Description Method : by describing in words
- Types of Sets:
- Singleton Sets: A set that has only one element is called a singleton set or also called a unit set. Example, Set A = { k | k is an integer between 3 and 5} which is A = {4}.
- Finite Sets: As the name implies, a set with a finite or countable number of elements is called a finite set. Example, Set B = {k | k is a prime number less than 20}, which is B = {2,3,5,7,11,13,17,19}
- Infinite Sets: A set with an infinite number of elements is called an infinite set. Example: Set C = {Multiples of 3}.
- Empty or Null Sets: A set that does not contain any element is called an empty set or a null set. An empty set is denoted using the symbol '∅'. It is read as 'phi'. Example: Set X = { }.
- Equal Sets: If two sets have the same elements in them, then they are called equal sets. Example: A = {1,2,3} and B = {1,2,3}. Here, set A and set B are equal sets. This can be represented as A = B.
- Unequal Sets: If two sets have at least one different element, then they are unequal sets. Example: A = {1,2,3} and B = {2,3,4}. Here, set A and set B are unequal sets. This can be represented as A ≠ B.
- Equivalent Sets:Two sets are said to be equivalent sets when they have the same number of elements, though the elements are different. Example: A = {1,2,3,4} and B = {a,b,c,d}. Here, set A and set B are equivalent sets since n(A) = n(B).
- Overlapping Sets: Two sets are said to be overlapping if at least one element from set A is present in set B. Example: A = {2,4,6} B = {4,8,10}. Here, element 4 is present in set A as well as in set B. Therefore, A and B are overlapping sets.
- Disjoint Sets: Two sets are disjoint if there are no common elements in both sets. Example: A = {1,2,3,4} B = {5,6,7,8}. Here, set A and set B are disjoint sets.
- Subset and Superset: For two sets A and B, if every element in set A is present in set B, then set A is a subset of set B(A ⊆ B) and in this case, B is the superset of set A(B ⊇ A). Example: Consider the sets A = {1,2,3} and B = {1,2,3,4,5,6}. Here: A ⊆ B, since all the elements in set A are present in set B.B ⊇ A denotes that set B is the superset of set A.
- Universal Set: A universal set is the collection of all the elements regarding a particular subject. The universal set is denoted by the letter 'U'. Example: Let U = {The list of all road transport vehicles}. Here, a set of cars is a subset for this universal set, the set of cycles, trains are all subsets of this universal set.
- Power Sets: Power set is the set of all subsets that a set could contain. Example: Set A = {1,2,3}. Power set of A is = {∅, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
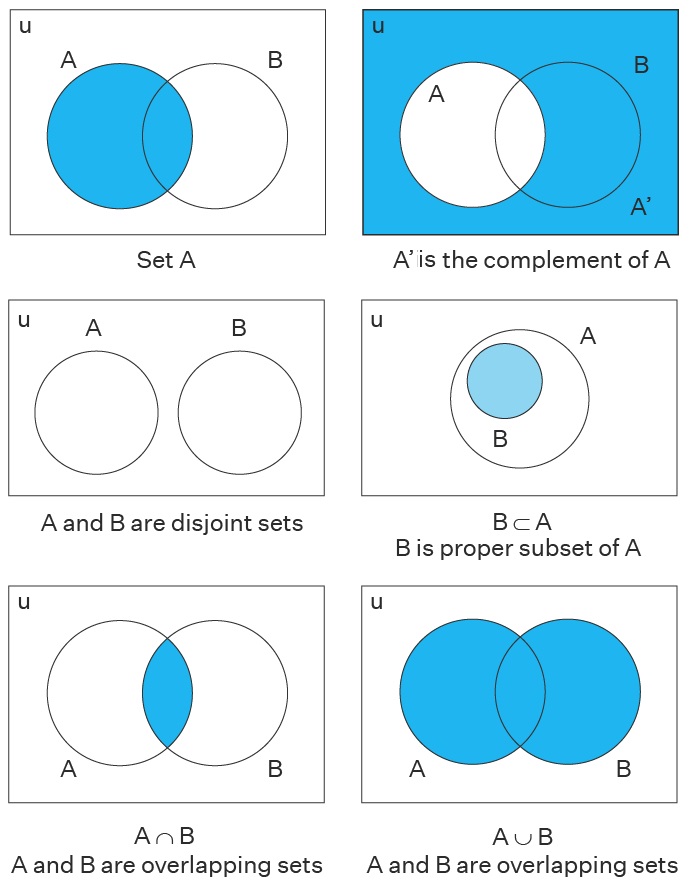
- Operations on Sets: Some important operations on sets in set theory include union, intersection, difference, the complement of a set, and the cartesian product of a set. A brief explanation of set operations is as follows.
-
- Union of Sets : Union of sets, which is denoted as A U B, lists the elements in set A and set B or the elements in both set A and set B. For example, {1, 3} ∪ {1, 4} = {1, 3, 4}
- Intersection of Sets: The intersection of sets which is denoted by A ∩ B lists the elements that are common to both set A and set B. For example, {1, 2} ∩ {2, 4} = {2}
- Set Difference: Set difference which is denoted by A - B, lists the elements in set A that are not present in set B. For example, A = {2, 3, 4} and B = {4, 5, 6}. A - B = {2, 3}.
- Set Complement: Set complement which is denoted by A', is the set of all elements in the universal set that are not present in set A. In other words, A' is denoted as U - A, which is the difference in the elements of the universal set and set A.
- Cartesian Product of Sets: The cartesian product of two sets which is denoted by A × B, is the product of two non-empty sets, wherein ordered pairs of elements are obtained. For example, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.
-
Sets Symbols : Set symbols are used to define the elements of a given set. The following table shows the set theory symbols and their meaning.
Symbols Meaning { } Symbol of set U Universal set n(X) Cardinal number of set X b ∈ A 'b' is an element of set A a ∉ B 'a' is not an element of set B ∅ Null or empty set A U B Set A union set B A ∩ B Set A intersection set B A ⊆ B Set A is a subset of set B B ⊇ A Set B is the superset of set A - Sets Formulas
- For any two overlapping sets A and B,
- n(A U B) = n(A) + n(B) - n(A ∩ B)
- n (A ∩ B) = n(A) + n(B) - n(A U B)
- n(A) = n(A U B) + n(A ∩ B) - n(B)
- n(B) = n(A U B) + n(A ∩ B) - n(A)
- n(A - B) = n(A U B) - n(B)
- n(A - B) = n(A) - n(A ∩ B)
For any two sets A and B that are disjoint,
- n(A U B) = n(A) + n(B)
- A ∩ B = ∅
- n(A - B) = n(A)
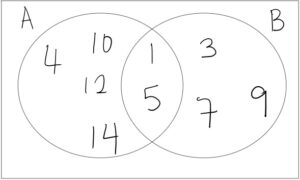
Question: Given the sets
A = {1,4,5,10,12,14};
B = {1,3,5,7,9}
- Find A U B and A ∩ B
- Draw a Venn Diagram to illustrate the data above.
Answer:
- A U B = {1,3,4,5,7,9, 10,12,14}
- A ∩ B = {1,5}
- Venn Diagram :
Let A = { x:x is a positive prime less than 15} and B = {x:x ∈N and 0< x-3<10), then find AUB and A ∩ B
Also represent it in Venn diagram
Ans:Union Operation on Sets :- Union combines the elements of two sets in one set, with no duplicate values.
+ve prime no starts from 2 So, A = { 2, 3, 5, 7, 11, 13 }
0< x-3<10 so 0< x <10+3 ⇒ 0< x <13
so B = { 4, 5, 6, 7, 8, 9, 10, 11, 12 }
⇒ A ∪ B = { 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11 ,12 , 13 }
Venn Diagram :-
Intersection operation on Sets :- It results in a set of elements which belong to both the sets. Or are common in both sets.
So, A = { 2, 3, 5, 7, 11, 13 } and B = { 4, 5, 6, 7, 8, 9, 10, 11, 12 }
⇒ A ⋂ B = { 5, 7, 11 }

