Key Concepts
Sets: A collection of well-defined objects. It is denoted by capital letters.
Example: A = {1, 2, 3, 4, 5..}.
Here, set A is a collection of all natural numbers.
Roster form of sets: All elements are written in curly braces { }, separated by commas.
Example: R = {1, 3, 7, 21, 2, 6, 14, 42}.
Set Builder Form: The elements of the set represent a common property.
Example, R = {x : x is a vowel in English alphabet}
First, let us see some questions based on the representation of sets.
Set Theory is the process of collection of objects, sets which are known as elements or numbers. For example:{1,2,3} is a set consisting of the numbers 1,2, and 3. Verbally, “3 is an element of the set {1,2,3}.”
To show this symbolically, use the symbol ∈, which is read as “is an element of” or “is a member of.” Therefore, you could have written:
3 ∈ {1,2,3}
A subset is a set contained within another set, or it can be the entire set itself. The set {1,2} is a subset of the set {1,2,3}, and the set {1,2,3} is a subset of the set {1,2,3}.
A ⊆ B if every element of A is also the element of B , we say that A is subset of B. Here B is called a superset of A.
If a set A has n elements, then the total number of subsets of A is = 2n
Proper subset : A is celled a proper subset of B if A ⊆ B and A ≠ B.
The number of proper subsets of the set {1, 2, 3} is = 2n -2 = 23 -2 = 6
Power Sets is the set of all subsets that a set could contain. Example: Set A = {1,2,3}. Power set of A is = {{∅}, {1}, {2}, {3}, {1,2}, {2,3}, {1,3}, {1,2,3}}.
If n ( A) =m , then Power set n{P(A)} = 2m
Example : Write all possible power subset of A = {2,3}.
All possible subset of A is = {{∅}, {2}, {3}, {2,3},
Thus , n(A)= 2 and n{P(A)} = 22 = 4
If A = {x, y} then the power set of A is = {f, {x}, {y}, {x, y}}
Singleton Sets : A set that has only one element is called a singleton set or also called a unit set. Example, Set A = { k | k is an integer between 3 and 5} which is A = {4}.
Empty or Null Sets : A set that does not contain any element is called an empty set or a null set. An empty set is denoted using the symbol '∅'. It is read as 'phi'. Example: Set X = {}.
Equal Sets :If two sets have the same elements in them, then they are called equal sets. Example: A = {1,2,3} and B = {1,2,3}. Here, set A and set B are equal sets. This can be represented as A = B.
Unequal Sets: If two sets have at least one element that is different, then they are unequal sets. Example: A = {1,2,3} and B = {2,3,4}. Here, set A and set B are unequal sets. This can be represented as A ≠ B.
Equivalent Sets: Two sets are said to be equivalent sets when they have the same number of elements, though the elements are different. Example: A = {1,2,3,4} and B = {a,b,c,d}. Here, set A and set B are equivalent sets since n(A) = n(B)
Overlapping Sets :Two sets are said to be overlapping if at least one element from set A is present in set B. Example: A = {2,4,6} B = {4,8,10}. Here, element 4 is present in set A as well as in set B. Therefore, A and B are overlapping sets.
Disjoint Sets :Two sets are disjoint sets if there are no common elements in both sets. Example: A = {1,2,3,4} B = {5,6,7,8}. Here, set A and set B are disjoint sets.
Since A and B are disjoint, \ A∩B=φ n(A∩B)=0 Now
Universal Set : A universal set is the collection of all the elements in regard to a particular subject. The universal set is denoted by the letter 'U'. Example: Let U = {The list of all road transport vehicles}. Here, a set of cars is a subset for this universal set, the set of cycles, trains are all subsets of this universal set.
Questions on Sets with Solutions
1. Write the solution set of the equation x2 – 4=0 in roster form.
Solution: x2 – 4 = x2 – 22 = (x – 2) (x + 2)
x = 2, -2
Thus, A = {-2, 2}
2. Write the set A = {1, 4, 9, 16, 25, . . . } in set-builder form.
Solution: If we see the pattern here, the numbers are squares of natural numbers, such as:
12 = 1
22 = 4
32 = 9
42 = 16
And so on.
A = {x : x is the square of a natural number}
Or we can write;
A = {x : x = n2 , where n ∈ N}
| Empty Set: A set with no elements. Also called a void set or null set
Finite & Infinite Set: A set with a definite number of elements (even with zero elements) is a finite set otherwise the set is infinite Equal sets: Two sets that have the same elements are called equal sets. |
3. Write an example of a finite and infinite set in set builder form.
Solution:
Finite set, A = {x : x ∈ N and (x – 1) (x – 2) = 0}
Infinite Set, B = {x : x ∈ N and x is prime}
4. Write an example of equal sets.
Solution: Let there be two sets A and B
A is the set of letters in “ALLOY”
B is the set of letters in “LOYAL”
Hence,
A = {A,L, O,Y}
B = {L,O,Y,A}
Therefore, in both sets, the elements are the same.
So, A = B.
| Subsets: A set A is said to be a subset of set B if every element of A is also an element of B
Symbolically, A ⊂ B if a ∈ A ⇒ a ∈ B. Power Set: Collection of all subsets of a set. |
5. Write the subsets of {1,2,3}.
Solution: Let A = {1, 2, 3}
The subsets of A are: φ, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, {1, 2, 3}
6. Write {x: x ∈ R, 3 ≤ x ≤ 4} as an interval.
Solution: {x: x ∈ R, 3 ≤ x ≤ 4} = [3, 4]
7. Write the interval (6, 12) in set builder form.
Solution:
Let A be the interval (6, 12).
The interval (6, 12) in set builder form is
A = {x: x ∈ R, 6 < x < 12}
8. If set A = {1, 3, 5}, B = {2, 4, 6} and C = {0, 2, 4, 6, 8}. Then write the universal set for all three sets.
Solution: If U is the universal set for sets A, B and C, then: U = Elements of set A + Elements of set B + Elements of set C
U = {0, 1, 2, 3, 4, 5, 6, 8}
Properties of Sets
There are six important properties of sets. Given, three sets A, B, and C, the properties for these sets are as follows.
| Property | Example |
|---|---|
| Commutative Property | A U B = B U A A ∩ B = B ∩ A |
| Associative Property | (A ∩ B) ∩ C = A ∩ (B ∩ C) (A U B) U C = A U (B U C) |
| Distributive Property | A U (B ∩ C) = (A U B) ∩ (A U C) A ∩ (B U C) = (A ∩ B) U (A ∩ C) |
| Identity Property | A U ∅ = A A ∩ U = A |
| Complement Property | A U A' = U |
| Idempotent Property | A ∩ A = A A U A = A |
Union of Sets : Union of sets, which is denoted as A U B, lists the elements in set A and set B or the elements in both set A and set B. For example, {1, 3} ∪ {1, 4} = {1, 3, 4}
Intersection of Sets : The intersection of sets which is denoted by A ∩ B lists the elements that are common to both set A and set B. For example, {1, 2} ∩ {2, 4} = {2}
Set Difference : Set difference which is denoted by A - B, lists the elements in set A that are not present in set B. For example, A = {2, 3, 4} and B = {4, 5, 6}. A - B = {2, 3}.
Q. If A = { 1, 2, 3, 4, 5, 6}, B = { 2, 4, 6, 8 }. Find A – B and B – A.
Solution: A – B = { 1, 3, 5 }
B – A = { 8 }
Clearly, A – B ≠ B – A
Set Complement : Set complement which is denoted by A', is the set of all elements in the universal set that are not present in set A. In other words, A' is denoted as U - A , which is the difference in the elements of the universal set and set A.
Q. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and A = {1, 3, 5, 7, 9}. Find A′.
Solution: A′ = { 2, 4, 6, 8, 10 }
Cartesian Product of Sets : The cartesian product of two sets which is denoted by A × B, is the product of two non-empty sets, wherein ordered pairs of elements are obtained. For example, {1, 3} × {1, 3} = {(1, 1), (1, 3), (3, 1), (3, 3)}.
Q. If A = {1, 2, 4}, B = {2, 4, 5}, C = {2, 5}, then (A - B) × (B - C) is
Q. If A = { 2, 4, 6, 8} and B = { 6, 8, 10, 12}. Find A ∪ B.
Solution: A ∪ B = { 2, 4, 6, 8, 10, 12}
Q. If A = { 2, 4, 6, 8} and B = { 6, 8, 10, 12}. Find A ∩ B.
Solution: A ∩ B = { 6, 8 }
Q. If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {5, 6, 7, 8}. Find A ∪ B ∪ C.
Solution: A ∪ B ∪ C = {1, 2, 3, 4, 5, 6, 7, 8}
Q. If A = {3, 5, 7, 9, 11}, B = {7, 9, 11, 13}, C = {11, 13, 15}. Find A ∩ (B ∪ C).
Solution:
As we know, A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
= {7, 9, 11} ∪ {11}
= {7, 9, 11}
Venn diagram : A Venn diagram is a diagram that helps us visualize the logical relationship between sets and their elements and helps us solve examples based on these sets.
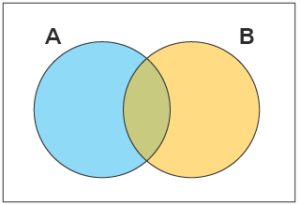
Sets Formulas
For any two overlapping sets A and B,
- n(A U B) = n(A) + n(B) - n(A ∩ B)
- n (A ∩ B) = n(A) + n(B) - n(A U B)
- n(A) = n(A U B) + n(A ∩ B) - n(B)
- n(B) = n(A U B) + n(A ∩ B) - n(A)
- n(A - B) = n(A U B) - n(B)
- n(A - B) = n(A) - n(A ∩ B)
- n (A U B U C) = n(A) + n(B) + n(C) - n(A ⋂ B) - n(B ⋂ C) - n(C ⋂ A) + n(A ⋂ B ⋂ C)
For any two sets A and B that are disjoint,
- n(A U B) = n(A) + n(B)
- A ∩ B = ∅
- n(A - B) = n(A)
Example:
Given the sets A={1,2,3},B={3,4} , C = {4, 5, 6}, then A∪(B∩C) is
Example:
Let's A = Even numbers from 1 to 25 = {2, 4,6,8,10,12,14,16,18,20,22,24}
and B = Multiple of 5 from 1 to 25 = {5,10,15 ,20, 25}
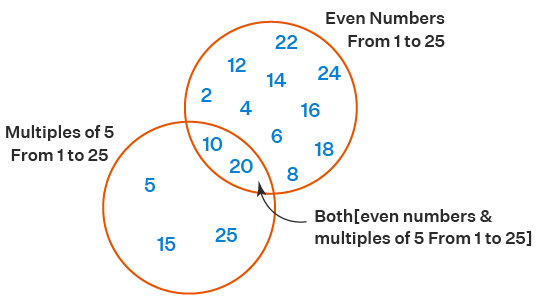
A U B = {2, 4,5, 6,8,10,12,14,15,16,18,20,22,24,25}
A ∩ B = {10,20}
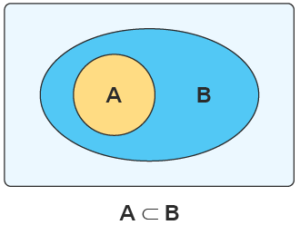
Let us understand the concept and the usage of the three basic Venn diagram symbols using the image given below.
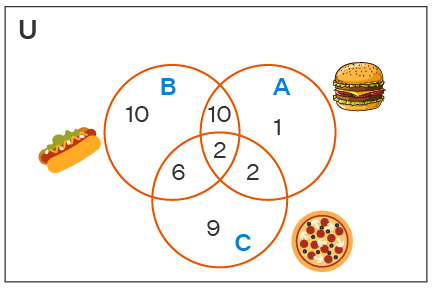
| Symbol | It refers to | Total Elements (No. of students) |
|---|---|---|
| A ∪ C | The number of students that prefer either burger or pizza or both. | 1 + 10 + 2 + 2 + 6 + 9 = 30 |
| A ∩ C | The number of students that prefer both burger and pizza. | 2 + 2 = 4 |
| A ∩ B ∩ C | The number of students that prefer a burger, pizza as well as hotdog. | 2 |
| Ac or A' | The number of students that do not prefer a burger. | 10 + 6 + 9 = 25 |
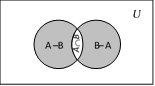
If A and B are two sets then (A − B) ∪ (B − A) ∪ (A ∩ B) is equal to
From Venn-Euler's diagram,
Example: In a cricket school, 12 players like bowling, 15 like batting, and 5 like both. Then how many players like either bowling or batting.
Solution:
Let A and B be the sets of players who like bowling and batting respectively. Then
n(A) = 12
n(B) = 15
n(A ⋂ B) = 5
We have to find n(A U B). Using the Venn diagram formula,
n(A U B) = n(A) + n(B) – n (A ⋂ B)
n(A U B) = 12 + 15 - 5 = 22.
Important Notes on Venn Diagrams:
Here is a list of a few points that should be remembered while studying Venn diagrams:
- Every set is a subset of itself i.e., A ⊆ A.
- A universal set accommodates all the sets under consideration.
- If A ⊆ B and B ⊆ A, then A = B
- The complement of a complement is the given set itself.
Let U = {x ϵ N : 1 ≤ x ≤ 8} be the universal set, N being the set of natural numbers. If A = {1, 2, 3, 4} and B = {2, 4, 6, 8}. Then what is the complement of (A – B) ?
Sol. A = {1, 2, 3, 4) B = {2, 4, 6, 8)
(A – B) = {1, 3}
(A – B)’ = U – (A – B)
= {1, 2, 3, 4, 5, 6, 7, 8} – {1, 3}
= {2, 4, 5, 6, 7, 8}
Let n(U) = 800, n(A) = 250, n(B) = 300, n(A∩B) = 350 then n(A’ ∩ B’) is equal to
Sol. n(A ∪ B) = n(A) + n(B) – n(A ∩ B)
= 250 + 300 – 350
= 200
n(A’ ∩ B’) = n(A ∪ B)’ = n(U) – n(A ∪B)
= 800 – 200
= 600
In a group of 500 students, there are 475 students who can speak Hindi and 200 can speak English. What is the number of students who can speak Hindi only ?
Sol. n(H) = 475, n(E) = 200, n (H ∪ E) = 500
n(H ∩ E) = n (H) + n(E) – n(H∪ E)
= 475 + 200 – 500 = 175.
Number of students who can speak Hindi only
= n(H) – n(H∩ E)
= 475 – 175 = 300
In a class of 120 students numbered 1 to 120, all even numbered students opt for Physics, those whose numbers are divisible by 5 opt for Chemistry and those whose numbers are divisible by 7 opt for Math. How many opt for none of the three subjects?
pproach: Let us find the number of students who took at least one of the three subjects and subtract the result from the overall 120 to get the number of students who did not opt for any of the three subjects.
Number of students who took at least one of the three subjects can be found by finding out n(A U B U C), where A is the set of students who took Physics, B is the set of students who took Chemistry and C is the set of students who opted for Math.
Now, n(A ∪ B ∪ C) = n(A) + n(B) + n(C) - {n(A ∩ B) + n(B ∩ C) + n(C ∩ A)} + n(A ∩ B ∩ C)
n(A) is the number of students who opted for Physics = 120/2 = 60
n(B) is the number of students who opted for Chemistry = 120/5 = 24
n(C) is the number of students who opted for Math = 120/7 = 17
Number of students who opted for Physics and Chemistry
Students whose numbers are multiples of 2 and 5 i.e., common multiples of 2 and 5 would have opted for both Physics and Chemistry.
The LCM of 2 and 5 will be the first number that is a multiple of 2 and 5. i.e., 10 is the first number that will be a part of both the series.
The 10th, 20th, 30th..... numbered students or every 10th student starting from student number 10 would have opted for both Physics and Chemistry.
Therefore, n(A ∩ B) = 120/10 = 12
Number of students who opted for Physics and Math
Students whose numbers are multiples of 2 and 7 i.e., common multiples of 2 and 7 would have opted for both Physics and Math.
The LCM of 2 and 7 will be the first number that is a multiple of 2 and 7. i.e., 14 is the first number that will be a part of both the series.
The 14th, 28th, 42nd..... numbered students or every 14th student starting from student number 14 would have opted for Physics and Math.
Therefore, n(C ∩ A) = 12/14 = 8
Number of students who opted for Chemistry and Math
Students whose numbers are multiples of 5 and 7 i.e., common multiples of 5 and 7 would have opted for both Chemistry and Math.
The LCM of 5 and 7 will be the first number that is a multiple of 5 and 7. i.e., 35 is the first number that will be a part of both the series.
The 35th, 70th.... numbered students or every 35th student starting with student number 35 would have opted for Chemistry and Math.
Therefore, n(B ∩ C) = 120/35 = 3
Number of students who opted for all three subjects
Students whose numbers are multiples of 2, 5, and 7 i.e., common multiples of 2, 5, and 7 would have opted for all 3 subjects.
The LCM of 2, 5, and 7 will be the first number that is a multiple of 2, 5, and 7. i.e., 70 is the first number that will be a part of all 3 series.
70 is the only multiple of 70 in the first 120 natural numbers. So, the 70th numbered student is the only one who would have opted for all three subjects.
Therefore, n(A ∪ B ∪ C) = 60 + 24 + 17 - (12 + 8 + 3) + 1 = 79.
n(A ∪ B ∪ C) is the number of students who opted for at least one of the 3 subjects.
Number of students who opted for none of the three subjects = 120 - n(A ∪ B ∪ C)
= 120 - 79 = 41.
Venn diagrams for some identities.
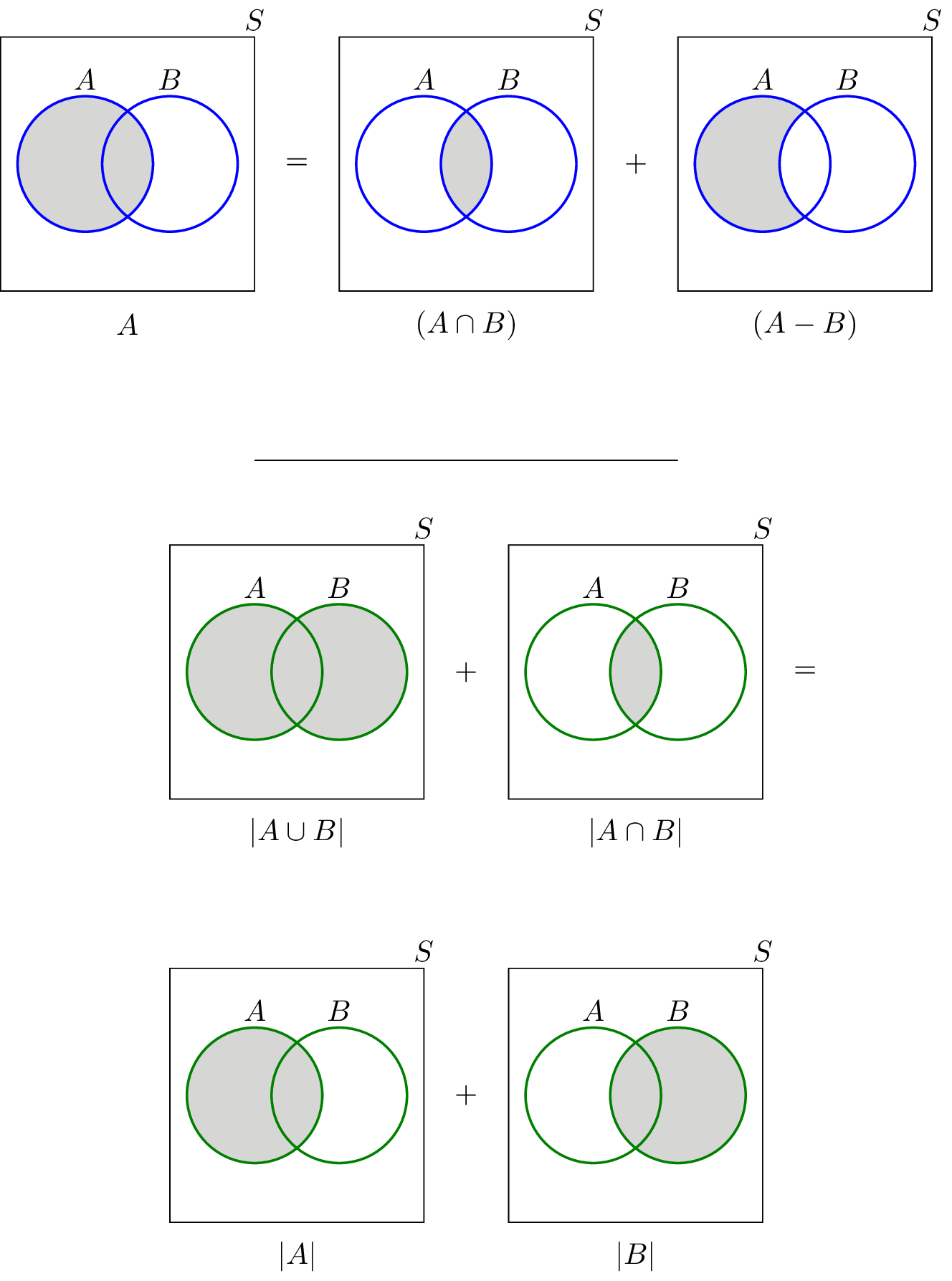
Out of 800 boys in a school, 224 played cricket, 240 played hockey and 336 played basketball. Of the total, 64 played both basketball and hockey; 80 played cricket and basketball and 40 played cricket and hockey; 24 played all the three games. The number of boys who did not play any game is?
Ans:
n(C)=224, n(H)=240, n(B)=336 , n(H∩B)=64, n(B∩C)=80 , n(H∩C)=40 , n(C∩H∩B)=24
Solution :
Let B, H, F denote the sets of members who are on the basketball team, hockey team and football team respectively. Then we are given
Hence, n(B∪H∪F)=(21+26+29)−(14+15+12)+8=43 Thus these are 43 members in all.
100=55+67−n(M∩P) / n(M∩P)=122−100=22
Now n (P only) =n(P)−n(M∩P) =67−22=45.
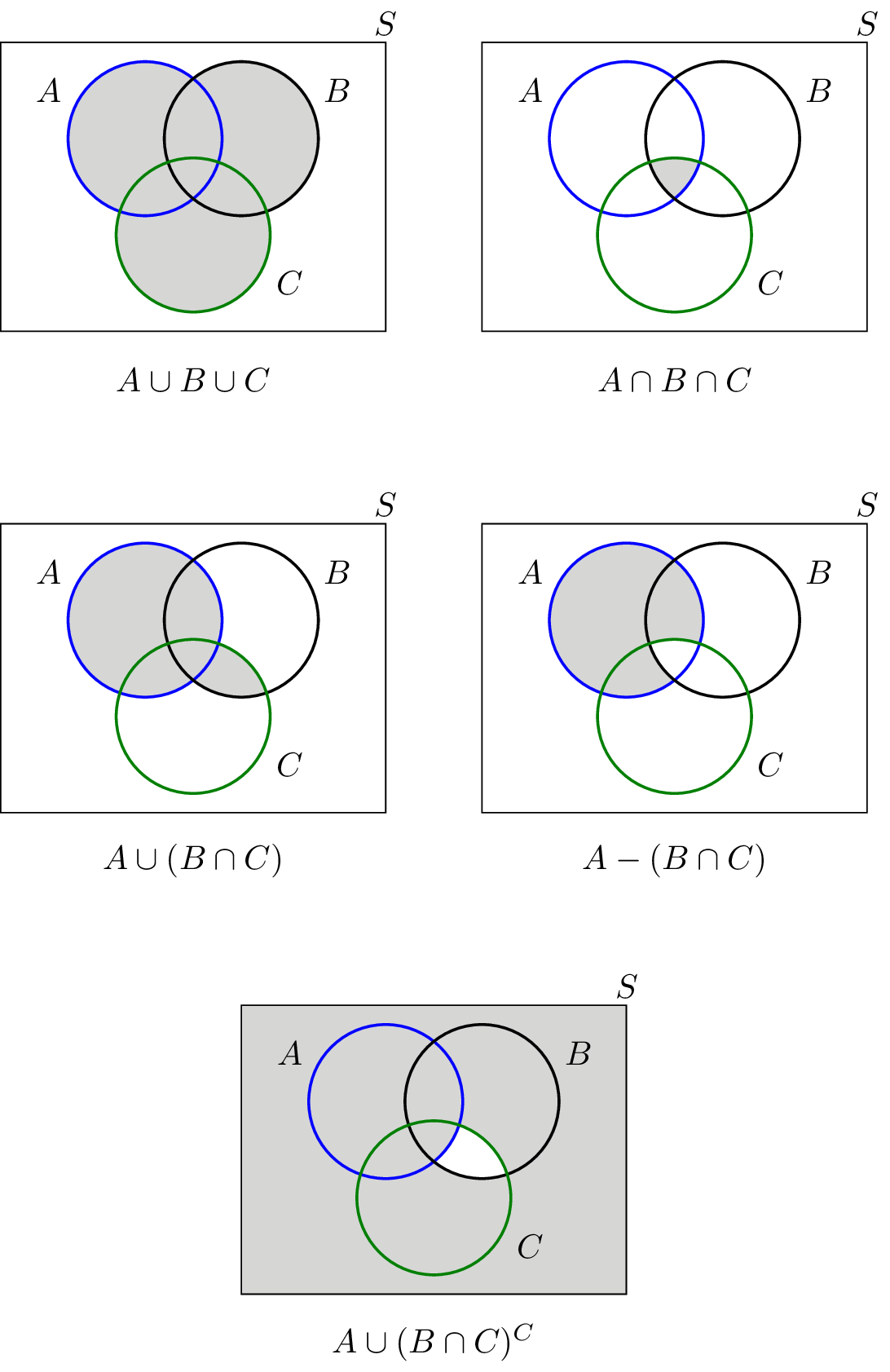
Let A, B, C be three sets as shown in the following Venn diagram. For each of the following sets, draw a Venn diagram and shade the area representing the given set.
- A∪B∪C
- A∩B∩C
- A∪(B∩C)
- A−(B∩C)
- A∪(B∩C)c
Q>If two sets A and B are having 99 elements in common, then the number of elements common to each of the sets A×B and B×A are:

