OVERVIEW

Concepts
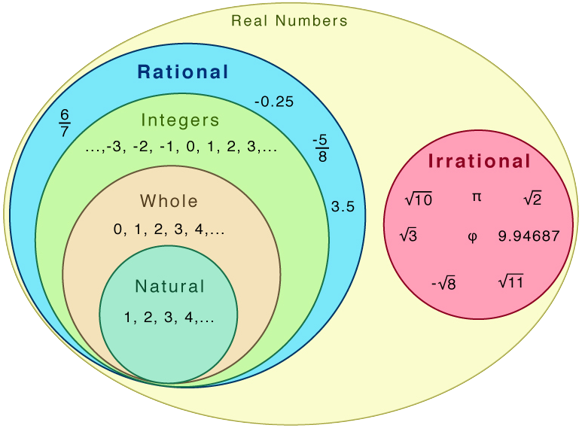
Points to remember:
- A number that can be expressed in the form p/q , where p and q are integers and q ≠ 0, is called a rational number.
- All integers and fractions are rational numbers.
- Any number that cannot be written as a rational number is, called an irrational number
- Natural numbers, whole numbers, integers, fractions of integers, and terminating decimals are rational numbers.
- Non-terminating decimals with repeating patterns of decimals, that is recurring decimals are also rational numbers.
- The word rational has evolved from the word ratio. In general, rational numbers are those numbers that can be expressed in the form of p/q, in which both p and q are integers and q≠0.
- A rational number a/b is said to be in standard form if a and b are integers having no common divisor other than 1 and b is positive.
- If a and b are any two rational numbers such that a < b then (a+b)/2 is a rational number lying between a and b.
- A rational number is said to be positive if its numerator and denominator are either both positive or both negative.
- A rational number is said to be negative if its numerator and denominator are of opposite signs.
The properties of rational numbers :
Closure Property ( rational numbers are closed under addition, subtraction and multiplication )
- The sum of two rational numbers is always a rational number. If a/b and c/d are any two rational numbers, then (a/b + c/d) is also a rational number. For example: (1/3)+(4/5) = 17/15
- The rational numbers are closed under subtraction. If a and b are any two rational numbers , then a – b is also a rational number. For example : (5/6) – (1/3) = 1/2
- The rational numbers are closed under multiplication. If a and b are any two rational numbers , then a x b is also a rational number. For example :(2/5) x (3/7) = 6/35
Commutative Property ( addition and multiplication are commutative but subtraction & division are not commutative)
- Two rational numbers can be added in any order. Thus for any two rational numbers a/b and c/d, we have (a/b + c/d) = (c/d + a/b). or we can say that (a+b) = (b+a)
- Two rational numbers can be multiplied in any order. We see that a x b= b x a
- Subtraction is not commutative for rational numbers. We see that a-b ≠ b-a
- Division is not commutative for rational numbers. We see that a /b ≠ b/a
Associative Property ( addition and multiplication are associative but subtraction & division are not associative)
- Addition and multiplication are associative for rational numbers
- While adding three rational numbers, they can be grouped in any order. Thus, for any three rational numbers a/b, c/d and e/f, we have (a/b + c/d) + e/f = a/b + (c/d + e/f). or we can say that a+( b+ c )=(a + b)+c
- While multiplying three rational numbers, a , b and c , we can say that a x ( b x c )=( a x b) x c
Distributive Property
- Any three rational numbers a, b and c, given in the form a x (b + c) is resolved as a x ( b + c ) = a x b + a x c. or a x (b−c)=a x b−a x c. This signifies that operand a is shared by the other two operands, b and c.
- Distributive property states that for any three numbers x, y and z we have x × ( y + z ) = (x × y) +( x × z)
Identity Property
- 0 is a rational number such that the sum of any rational number and 0 is the rational number itself. Thus, (a/b + 0) = (0 + a/b) = a/b, for every rational number a/b
- 0 is called the additive identity for rationals.
Inverse Property
- For every rational number a/b, there exists a rational number –a/b such that (a/b + -a/b) = {a + (-a)}/b = 0/b = 0 and similarly, (-a/b + a/b) = 0. Thus, (a/b + -a/b) = (-a/b + a/b) = 0.
- -a/b is called the additive inverse of a/b
Types of Rational Numbers
The different types of rational numbers are given as follows.
- Integers like -2, 0, 3, etc., are rational numbers.
- Fractions whose numerators and denominators are integers like 3/7, -6/5, etc., are rational numbers.
- Terminating decimals like 0.35, 0.7116, 0.9768, etc., are rational numbers.
- Non-terminating decimals with some repeating patterns (after the decimal point) such as 0.333..., 0.141414..., etc., are rational numbers. These are popularly known as non-terminating repeating decimals.
Example: Is 0.923076923076923076923076923076... a rational number?
Solution: The given number has a set of decimals 923076 which is recurring and repeated continuously. Thus, it is a rational number.
Let us take another example.
Example: Is √2 a rational number?
Solution: If we write the decimal value of √2 we get √2 = 1.414213562....which is a non-terminating and non-recurring decimal. Therefore, this is not a rational number. It is an irrational number.
Is 0 a Rational Number?
Yes, 0 is a rational number as it can be written as a fraction of integers like 0/1, 0/-2,... etc. In other words, 0/5 = 0, 0/-2 = 0, 0/1 = 0, and so on.
Adding and Subtracting Rational Numbers
For adding and subtracting rational numbers, we use the same rules of addition and subtraction of integers. Let us understand this with the help of an example.
Example: Solve 1/2 - (-2/3)
Solution: Let us solve this using the following steps:
- Step 1: As we simplify 1/2 - (-2/3), we will follow the rule of addition and subtraction of numbers which says that the subtraction fact can change to an addition fact and the sign of the subtrahend gets reversed. This will make it 1/2 + 2/3
- Step 2: Now, we need to add these fractions 1/2 + 2/3
- Step 3: Using the rules of addition of fractions, we will convert the given fractions to like fractions to get common denominators so that it becomes easier to add them. For this, we need to find the LCM of the denominators 2 and 3 which is 6. Then we will convert the fractions to their respective equivalent fractions which will make them 3/6 + 4/6. This will give the sum as 7/6 which can be written in the form of a mixed fraction 116116
Multiplying and Dividing Rational Numbers
The multiplication and division of rational numbers can be done in the same way as fractions. To multiply any two rational numbers, we multiply their numerators and their denominators separately and simplify the resultant fraction. Let us understand this with the help of an example.
Example: Multiply 3/5 × -2/7
Solution: Let us solve this using the following steps:
- Step 1: In order to multiply 3/5 × (-2)/7, we will first multiply the numerators and then multiply the denominators.
- Step 2: In this case, when we multiply the numerators, it will be 3 × (-2) = -6.
- Step 3: When we multiply the denominators, it will be 5 × 7 = 35. Therefore, the product will be -6/35.
When we need to divide any two fractions, we multiply the first fraction (which is the dividend) by the reciprocal of the second fraction (which is the divisor). Let us understand this with the help of an example.
Example: Divide 3/5 ÷ 2/7
Solution: Let us solve this using the following steps:
- Step 1: In order to divide 3/5 ÷ 2/7, we will first write the reciprocal of the second fraction. This will make it 3/5 × 7/2
- Step 2: Now, we will multiply the numerators This will be 3 × 7 = 21.
- Step 3: Then, we will multiply the denominators, it will be 5 × 2 = 10. Therefore, the product will be 21/10.
Find the additive inverse of the following:
(i) 22/4 (ii) ⅜ (iii) – 24/–5 (iv) 17/(– 6)
Solution:
(i) 22/4
The additive inverse of 22/4 is – 22/4 or – 11/2.
(ii) ⅜
The additive inverse of ⅜ is – ⅜.
(iii) – 24/–5
The additive inverse of –24/–5 or 24/5 is – 24/5.
(iv) 17/(– 6)
The additive inverse of 17/(–6) or – 17/6 is 17/6.
Find the multiplicative inverse of the following:
(i) 18/7 (ii) 34/6 (iii) 29/3 (iv) –6/7
Solution:
(i) 18/7
The multiplicative inverse of 18/7 is 7/18.
(ii) 34/6
The multiplicative inverse of 34/6 is 6/34 or 3/17.
(iii) 29/3
The multiplicative inverse of 29/3 is 3/29.
(iv) –6/7
The multiplicative inverse of –6/7 is –7/6.
State true or false for the following:
(i) Rational numbers are closed with respect to division.
(ii) Every whole number is a rational number.
(iii) Every integer is a rational number.
(iv) There are infinitely many rational numbers between any two rational numbers.
(v) 1 and –1 are the only rational numbers which are equal to their reciprocal.
Solution:
(i) Rational numbers are closed with respect to division. (False)
(ii) Every whole number is a rational number. (True)
(iii) Every integer is a rational number. (False)
(iv) There are infinitely many rational numbers between any two rational numbers. (True)
(v) 1 and –1 are the only rational numbers which are equal to their reciprocal. (True)
Find five rational numbers between ⅔ and ⅘ .
Solution:
We have the equivalent fractions,
⅔ = (2 × 5)/(3 × 5) = 10/15 and ⅘ = (4 × 3)/(5 × 3) = 12/15
To find five rational numbers lets multiply both numerator and denominator of the equivalent fractions by 5, we get
(10 × 5)/(15 × 5) = 50/75 and (12 × 5)/(15 × 5) = 60/75
Therefore, five rational numbers between ⅔ = 50/75 and ⅘ = 60/75 are
51/75, 52/75, 53/75, 54/75, 55/75.
State which property is in the following:
(i) ⅖ + ( –⅚ + ½) = {⅖ + ( –⅚)} + ½
(ii) 3 – 45/7 + 3/2 = (3 + 3/2) – 45/7
(iii) 300 × 45 = (300 × 40) + (300 × 5)
(iv) 2/19 × 19/2 = 1
(v) 3/7 + (–3/7) = 0
Solution:
| (i) ⅖ + ( –⅚ + ½) = {⅖ + ( –⅚)} + ½ | Associativity |
| (ii) 3 – 45/7 + 3/2 = (3 + 3/2) – 45/7 | Commutativity and associativity |
| (iii) 300 × 45 = (300 × 40) + (300 × 5) | Distributivity of multiplication over addition |
| (iv) 2/19 × 19/2 = 1 | Multiplicative inverse |
| (v) 3/7 + (–3/7) = 0 | Additive inverse |
Find ten rational numbers between 2 and 3.
Solution:
Multiply and divide both the numbers by 11, we get
(2 × 11)/11 = 22/11 and (3 × 11)/11 = 33/11
Rational numbers between 2 = 22/11 and 3 = 33/11 are:
23/11, 24/11, 25/11, 26/11, 27/11, 28/11, 29/11, 30/11, 31/11, 32/11.
From a 50 m cloth, 7/3 m cloth cut out to make a shirt and 14/5 is cut out to make a curtain. Find the remaining length of the cloth?
Solution:
Total length of the cloth = 50 m
Cloth used for making shirt = 7/3 m
Cloth used for making curtain = 14/5 m
Remaining cloth = 50 – 7/3 – 14/5 = 50 – {7/3 + 14/5}
= 50 – {77/15} = (750 – 77)/15 = 673/15 m





![]()




A train covers 256 km in an hour. How much distance it would cover in 35/8 hours?
Solution:
Distance covered by the train in one hour = 256 km
Distance covered in 35/8 hours = 256 × 35/8 = 1120 km
The monthly salary of a man is ₹ 65000, one-fifth of his salary is spend paying the rent, 5/26th of his remaining salary is spent in buying groceries, and half of the rest salary is spent miscellaneous expenses. How much his monthly saving?
Solution:
Total salary = ₹ 65000
Amount spend in paying the rent = ⅕ × 65000 = ₹ 13000
Remaining amount = 65000 – 13000 = ₹ 52000
Amount spend in groceries = 5/26 × 52000 = ₹ 10000
Remaining amount = 52000 – 10000 ₹ 42000
Miscellaneous expenses = ½ × 42000 = ₹ 21000
∴ his monthly savings = ₹ 21000.
Short Answer Type Questions:
What are the multiplicative and additive identities of rational numbers?
Solution: 0 and 1 are the additive and multiplicative identity of rational numbers respectively.
Write the additive inverse of 19/-6 and -⅔
Solution: 19/-6 = 19/6 and -⅔ = 2/3
Write the multiplicative inverse of -13/19 and -7
Solution: -13/19 = -19/13 and -7 = -1/7
Mention a rational number which has no reciprocal.
Solution: A rational number “0” has no reciprocal or multiplicative inverse.
Mention any 4 rational numbers which are less than 5.
Solution: -1, 1, 2 and 3.
Long Answer Type Questions:
Mention the commutativity, associative and distributive properties of rational numbers. Also, check a × b = b × a and a + b = b + a for a = ½ and b = ¾
Solution:
Commutative property:
For any two rational numbers a and b, a + b = b + a.
For any two rational numbers a and b, a × b = b × a.
Associative Property:
For any three rational numbers a, b and c,
(a + b) + c = a + (b + c)
Distributive property states that for any three numbers x, y and z,
x × ( y + z ) = (x × y) + ( x × z)
a*b = b*a
a*b = ½ * ¾ = 3/8
b*a = ¾ * ½ = 3/8
a + b = ¾ + ½ = 5/4
b + a = ½ + ¾ = 5/4
Write any 5 rational numbers between −2/5 and ½.
Solution:
−2/5 can be written as −8/20.
1/2 can be written as 10/20.
So, rational numbers between these two numbers can be,
−7/20,−6/20,−5/20,−4/20,−3/20,−2/20,−1/20,0,1/20,2/20,3/20,4/20.
If the product of any two rational numbers is 2 and one of them is 1/7, find the other?
Solution: Consider 2 rational numbers as “a” and “b”.
Given, a = 1/7 and a × b = 2
Now, 1/7 × b = 2
⇒ b = 7 × 2 = 14
So, the other rational number will be 14.
Mr. X went shopping with a certain amount of money. He spent Rs. 10(¼) on buying a pen and Rs. 25(¾) in food. He then gave the remaining Rs. 16(½) to his friend. Calculate how much money he initially had.
Solution: To get the amount of money Mr X had initially, his purchases have to be added.
So,
Initial Money = 10(¼) + 25(¾) + 16(½)
= 41/4 + 103/4 + 33/2
By taking LCM, we get
Initial Money = 105/2
Represent −𝟐/𝟏𝟏, −𝟓/𝟏𝟏, and −𝟗/ 𝟏𝟏 on the number line.
Solution: To represent these numbers, divide the number line into 11 parts. Now, the given rational numbers will be 2, 5 and 9 points away from 0.

Answer following questions :
1.From the choices given below mark the co-prime numbers
| 1. (a) | 2. (c) | 3. (a) | 4. (d) | 5. (d) |
| 6. (d) | 7. (b),(c) | 8. (d) | 9. (d) | 10. (c) |
| 11. (c) | 12. (a) | 13. (c) | 14. (b) | 15. (b) |
| 16. (d) | 17. (b) | 18. (d) | 19. (a) | 20. (c) |
Click here to join online test to understand the concept and clear your doubts.
Mock Test
If you are interested to join online classes & online test series to clear your doubts Register Now!

