Key Concept
- Quadratic Polynomial: A polynomial, whose degree is 2, is called a quadratic polynomial. It is in the form of p(x) = ax2 + bx + c, where a ≠ 0
- Quadratic Equation: When we equate the quadratic polynomial to zero then it is called a Quadratic Equation i.e. if p(x) = 0, then it is known as Quadratic Equation.
- Standard form of Quadratic Equation :
-
-
-
-

- where a, b, c are the real numbers and a≠0
-
-
-
-
- Types of Quadratic Equations
- Complete Quadratic Equation => ax2 + bx + c = 0, where a ≠ 0, b ≠ 0, c ≠ 0
- Pure Quadratic Equation => ax2 = 0, where a ≠ 0, b = 0, c = 0
- Roots of a Quadratic Equation
Let x = α where α is a real number. If α satisfies the Quadratic Equation ax2+ bx + c = 0 such that aα2 + bα + c = 0, then α is the root of the Quadratic Equation.As quadratic polynomials have degree 2, therefore Quadratic Equations can have two roots. So the zeros of quadratic polynomial p(x) =ax2+bx+c is same as the roots of the Quadratic Equation ax2+ bx + c= 0. - Methods to solve the Quadratic Equations
There are three methods to solve the Quadratic Equations-
1.0) Factorisation Method
In this method, we factorise the equation into two linear factors and equate each factor to zero to find the roots of the given equation.Step 1: Given Quadratic Equation in the form of ax2 + bx + c = 0.
Step 2: Split the middle term bx as mx + nx so that the sum of m and n is equal to b and the product of m and n is equal to ac.
Step 3: By factorization we get the two linear factors (x + p) and (x + q)
ax2 + bx + c = 0 = (x + p) (x + q) = 0
Step 4: Now we have to equate each factor to zero to find the value of x.

These values of x are the two roots of the given Quadratic Equation.
2.0) Completing the square method
In this method, we convert the equation in the square form (x + a)2 - b2 = 0 to find the roots.
Step1: Given Quadratic Equation in the standard form ax2 + bx + c = 0.
Step 2: Divide both sides by a

Step 3: Transfer the constant on RHS then add square of the half of the coefficient of x i.e. on both sides
on both sides


Step 4: Now write LHS as perfect square and simplify the RHS.

Step 5: Take the square root on both the sides.

Step 6: Now shift all the constant terms to the RHS and we can calculate the value of x as there is no variable at the RHS.

3.0) Quadratic formula method
In this method, we can find the roots by using quadratic formula. The quadratic formula is
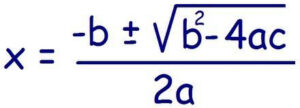
where a, b and c are the real numbers and b2 – 4ac is called discriminant.
To find the roots of the equation, put the value of a, b and c in the quadratic formula.
Nature of Roots
From the quadratic formula, we can see that the two roots of the Quadratic Equation are -

Where D = b2 – 4ac
The nature of the roots of the equation depends upon the value of D, so it is called the discriminant.

∆ = Discriminant

Examples: Which of the following is a quadratic equation?
a. x² + 2x + 1 = (4 - x)² + 3
b. -2x² = (5 - x)(2x - 2/5)
c. (k + 1)x² + (3/2)x = 7 where k = -1
d. x³ - x² = (x - 1)³
Solution:
We have to find the quadratic equation.
The standard form of a quadratic equation is ax2 + bx + c = 0 in variable x.
Where a, b, and c are real numbers and a ≠ 0.
We need to check if the degree of the given equations is 2.
From the options,
A) x² + 2x + 1 = (4 - x)² + 3
By using algebraic identity,
(a - b)² = a² - 2ab + b²
x² + 2x + 1 = 16 + x² - 8x + 3
By grouping,
x² - x² + 2x + 8x + 1 - 16 - 3 = 0
10x - 18 = 0
The degree of the equation is 1.
Therefore, x² + 2x + 1 = (4 - x)² + 3 is not a quadratic equation.
B) -2x² = (5 - x)(2x - 2/5)
-2x² = (5 - x)(10x - 2)/5
-10x² = (5 - x)(10x - 2)
By multiplicative and distributive property,
-10x² = 50x - 10 - 10x² + 2x
By grouping,
-10x² + 10x² + 52x - 10 = 0
52x - 10 = 0
The degree of the equation is 1.
Therefore, -2x² = (5 - x)(2x - 2/5) is not a quadratic equation.
C) (k + 1)x² + (3/2)x = 7 where k = -1
(-1 + 1)x² + (3/2)x = 7
3/2x = 7
The degree of the equation is 1.
Therefore, (k + 1)x² + (3/2)x = 7 where k = -1 is not a quadratic equation.
D) x³ - x² = (x - 1)³
By using algebraic identity,
(a - b)³ = a³ - b³ - 3a²b + 3ab²
x³ - x² = x³ - 1 - 3x² + 3x
By grouping,
x³ - x³ - x² + 3x² - 3x + 1 = 0
2x² - 3x + 1 = 0
The degree of the equation is 2.
Therefore, x³ - x² = (x - 1)³ is a quadratic equation.
✦ Try This: Which of the following is a quadratic equation?
- x² + 2x + 1 = (4 - x)² + 3
- -2x² = (5 - x)(2x - 2/5)
- (k + 1)x² + (3/2)x = 7 where k = -1
- x² + 3x = (-1) (1 - 3x)²
Check whether the following are quadratic equations:
(i) (x + 1)2 = 2(x - 3)
ii) x2 - 2x = (-2)(3 - x)
iii) (x - 2)(x + 1) = (x - 1)(x + 3)
iv) (x - 3)(2x +1) = x(x + 5)
v) (2x -1)(x - 3) = (x + 5)(x -1)
vi) x2 + 3x +1 = (x - 2)2
vii) (x + 2)3 = 2x (x2 -1)
viii) x3 - 4x2 - x +1 = (x - 2)3
Solution:
Standard form of a quadratic equation is ax2 + bx + c = 0 in variable x where a, b, and c are real numbers and a ≠ 0. We need to check if the degree of the given equations is 2.
(i) (x + 1)2 = 2(x - 3)
Since (a + b)2 = a2 + b2 + 2ab
x2 + 2x + 1 = (2x - 6)
x2 + 2x + 1 - (2x - 6) = 0
x2 + 2x + 1 - 2x + 6 = 0
x2 + 7 = 0
Here, the degree of x2 + 7 = 0 is 2.
∴ It is a quadratic equation.
(ii) x2 - 2x = (-2) (3 - x)
x2 - 2x = - 6 + 2x
x2 - 2x - 2x + 6 = 0
x2 - 4x + 6 = 0
Degree = 2
∴ It is a quadratic equation.
iii) (x - 2)( x + 1) = (x -1)( x + 3)
x2 - 2x + x - 2 = x2 + 3x - x - 3
x2 - x - 2 = x2 + 2x - 3
x2 - x - 2 - x2 - 2x + 3 = 0
-3x + 1 = 0
Degree = 1
∴ It is not a quadratic equation.
iv) (x - 3)(2x +1) = x ( x + 5)
2x2 + x - 6x - 3 = x2 + 5x
2x2 - 5x - 3 = x2 + 5x
2x2 - 5x - 3 - x2 - 5x = 0
x2 - 10x - 3 = 0
Degree = 2
∴ It is a quadratic equation.
v) (2x -1)(x - 3) = (x + 5)(x -1)
2x2 - 6x - x + 3 = x2 - x + 5x - 5
2x2 - 7x + 3 = x2 + 4x - 5
2x2 - 7x + 3 - x2 - 4x + 5 = 0
x2 - 11x + 8 = 0
Degree = 2
∴ It is a quadratic equation
vi) x2 + 3x +1 = (x - 2)2
x2 + 3x +1 = x2 - 4x + 4 [∵ (a - b)2 = a2 - 2ab + b2]
x2 + 3x + 1 - x2 + 4x - 4 = 0
7x - 3 = 0
Degree = 1
∴ It is not a quadratic equation.
vii) (x + 2)3 = 2x (x2 -1)
We know that, (a + b)3 = a3 + 3a2b + 3ab2 + b3
x3 + 3x2 (2) + 3(x)(2)2 + (2)3 = 2x3 - 2x
x3 + 6x2 + 12x + 8 = 2x3 - 2x
- x3 + 6x2 + 14x + 8 = 0
Degree = 3
∴ It is not a quadratic equation.
viii) x3 - 4x2 - x + 1 = (x - 2)3
x3 - 4x2 - x + 1 = x3 - 3(x)2(2) + 3(x)(2)2 - (2)3 [∵ (a - b)3 = a3 - 3a2b + 3ab2 - b3]
x3 - 4x2 - x + 1 = x3 - 6x2 + 12x - 8
x3 - 4x2 - x + 1 - x3 + 6x2 - 12x + 8 = 0
2x2 - 13x + 9 = 0
Degree = 2
∴ It is a quadratic equation
Find the roots of the following quadratic equations by factorization:
(i) x2 - 3x -10 = 0
(ii) 2x2 + x - 6 = 0
(iii) √2x2 + 7x + 5√2 = 0
(iv) 2x2 - x + 1/ 8 = 0
(v) 100x2 - 20x + 1= 0
Solution:
The roots of the polynomial are the same as the zeros of the polynomial.
Therefore, roots can be found by factorizing the quadratic equation into two linear factors and after that equating each factor to zero.
(I) x2 - 3x -10 = 0
x2 - 5x + 2x -10 = 0
x(x - 5) + 2(x - 5) = 0
(x - 5) (x + 2) = 0
x - 5 = 0 and x + 2 = 0
x = 5 and x = - 2
Therefore, roots are : - 2, 5
(ii) 2x2 + x - 6 = 0
2x2 + 4x - 3x - 6 = 0
2x (x + 2) - 3 (x + 2) = 0
(2x - 3) (x + 2) = 0
2x - 3 = 0 and x + 2 = 0
2x = 3 and x = - 2
x = 3/2 and x = - 2
Therefore, roots are: 3/2, -2
(iii) √2x2 + 7x + 5√2 = 0
√2x2 + 5x + 2x + 5√2 = 0
√2x2 + 2x + 5x + 5√2 = 0
(√2x + 5) (x + √2) = 0
√2x + 5 = 0 or x + √2 = 0
√2x = - 5 or x = - √2
x = - 5/√2 or x = - √2
Therefore, roots are: - 5/√2, - √2
(iv) 2x2 - x + 1/ 8 = 0
Multiplying both sides of the equation by 8:
2(8) x2 - 8(x) + (8)(1/ 8) = (0)8
16x2 - 8x + 1 = 0
16x2 - 4x - 4x + 1 = 0
4x (4x - 1) -1 (4x - 1) = 0
(4x - 1) (4x - 1) = 0
(4x - 1)2 = 0
4x - 1 = 0
x = 1/4 and x = 1/4
Roots are: 1/4, 1/4
(v) 100x2 - 20x + 1 = 0
100x2 - 20x + 1 = 0
100x2 - 10x - 10x + 1 = 0
10x(10x - 1) -1(10 x - 1) = 0
(10x - 1)(10 x - 1) = 0
(10x - 1)2 = 0
10x - 1 = 0
x =1/10 and x = 1/10
Roots are: 1/10, 1/10
Find the roots of the quadratic equation 3x2 - 2√6x + 2 = 0
Solution :
Let us find the roots by splitting the middle term.
Given, 3x2 - 2√6x + 2 = 0
Split bx into such a way that it is equal to a×c.
- 2√6x can be split into- √6x and - √6x . [ ∵ (- √6x) × (- √6x) = 6x2].
⇒ 3x2 - 2√6x + 2 = 0 can be written as 3x2 - √6x - √6x + 2 = 0.
Take out the common factors,
⇒ √3x (√3x - √2) - √2 (√3x - √2)
⇒ (√3x - √2)(√3x - √2)
Put both the equations equal to 0
⇒ √3x - √2 = 0 and √3x - √2 = 0
⇒ x = √⅔
Since the roots are repeated twice, the roots of the equation are √⅔ , √⅔
(i) The area of a rectangular plot is 528 m2. The length of the plot (in meters) is one more than twice its breadth. We need to find the length and breadth of the plot.
(ii) The product of two consecutive positive integers is 306. We need to find the integers.
(iii) Rohan’s mother is 26 years older than him. The product of their ages (in years) 3 years from now will be 360. We would like to find Rohan’s present age.
(iv) A train travels a distance of 480 km at a uniform speed. If the speed had been 8 km/h less, then it would have taken 3 hours more to cover the same distance. We need to find the speed of the train.
Solution:
(i) We know that the area of a rectangle can be expressed as the product of its length and breadth.
Since we don’t know the length and breadth of the given rectangle, we assume the breadth of the plot to be a variable (x meters). Then, we use the given relationship between length and breadth: length = 1 + 2 times breadth.
Therefore, Length = 2x + 1
Area of rectangle = Length × Breadth
Breadth = x
Length = 2x + 1
Area of Rectangular Plot = Length × Breadth = 528 m2
(2x + 1) × (x) = 528
2x2 + x = 528
2x2 + x - 528 = 0
Thus, the quadratic equation is 2x2 + x - 528 = 0 , where x is the breadth of the rectangular plot.
(ii) Let the first integer be x.
Since the integers are consecutive, the next integer is (x + 1).
It is given that
First integer × Next integer = 306
Therefore,
x (x + 1) = 306
x (x +1) = 306
x2 + x = 306
x2 + x - 306 = 0
Thus, the quadratic equation is x2 + x - 306 = 0 where x is the first integer.
(iii) Let's assume that Rohan’s present age is x years. Then, from the first condition, his mother’s age is (x + 26) years.
Three years from now, Rohan’s age will be (x + 3) and Rohan’s mother age will be (x + 3) + 26 = (x + 29). The product of their ages is 360.
Therefore,
(x + 3) × (x + 29) = 360
x2 + 29x + 3x + 87 = 360
x2 + 32x + 87 - 360 = 0
x2 + 32x - 273 = 0
Thus, the quadratic equation is x2 + 32x - 273 = 0 where x is the present age of Rohan.
(iv) Distance is equal to speed multiplied by time. Let the speed be s km/h and time be t hours.
D = st
480 = st …(i)
t = 480/s …(ii)
As per the given conditions, for the same distance covered at a speed reduced by 8 km/h, the time taken would have increased by 3 hours.
Therefore,
(s - 8)(t + 3) = 480
st + 3s - 8t - 24 = 480
480 + 3s - 8 (480/s) - 24 = 480 [From equations (i) and (ii)]
3s - 3840/s - 24 = 0
3s (s) - 3840 - 24 (s) = 0
3s2 - 24s - 3840 = 0
(3s2 - 24s - 3840)/3 = 0
s2 - 8s - 1280 = 0
Thus, the quadratic equation is s2 - 8s - 1280 = 0, where s is the speed of the train.
Find two numbers whose sum is 27 and product is 182.
Solution:
Let us find the 2 numbers whose sum is 27 and product is 182.
For this, let us consider one of the numbers to be x. Then the other number will be 27 - x.
The product of the two numbers is given as 182. This means in terms of x this can be expressed as, x(27 - x) = 182
This can be written in the form of the following quadratic equation:
x(27 - x) = 182
x(27 - x) = 182
27x - x2 = 182
27x - x2 - 182 = 0
x2 - 27 x + 182 = 0 [Rearranging the terms and multiplying both sides by negative sign]
x2 - 14x - 13x + 182 = 0
x (x - 14) - 13 (x - 14) = 0
(x -13) (x - 14) = 0
x - 13 = 0 and x - 14 = 0
x = 13 and x = 14
A cottage industry produces a certain number of pottery articles in a day. It was observed on a particular day that the cost of production of each article (in rupees) was 3 more than twice the number of articles produced on that day. If the total cost of production on that day was ₹ 90, find the number of articles produced and the cost of each article.
Solution:
Let the number of articles produced in one day be x.
Therefore, the cost (in rupees) of each article will be (3 + 2x)
The total cost of production = Cost of each article × Total number of articles
Let us use this relation to form a quadratic equation.
(3 + 2x) ( x) = 90
3x + 2x2 = 90
2x2 + 3x - 90 = 0
2x2 + 15x - 12x - 90 = 0
x(2x + 15) - 6(2x + 15) = 0
(2x + 15) (x - 6) = 0
2x + 15 = 0 and x - 6 = 0
2x = -15 and x = 6
x = -15/2 and x = 6
Number of articles cannot be a negative number.
Therefore, x = 6
Cost of each article = 3 + 2x
= 3 + 2 (6)
= Rs.15
Cost of each article is Rs.15.
Number of articles produced is 6.

