Concepts
Construct a Quadrilateral
When:
- Four sides and one diagonal are given.
- Two diagonals and three sides are given.
- Two adjacent sides and three angles are given.
- Three sides and two included angles are given.
- Other specific properties are known.
1. Construct quadrilaterals when four sides and one diagonal is given.
Construct a quadrilateral PQRS where PQ = 4 cm, Oq = 6 cm, RS = 5 cm, PS = 5.5 cm and PR= 7 cm
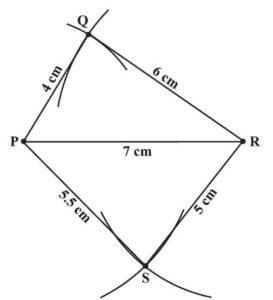
- Draw Δ PQR using SSS construction condition.
- With P as the centre, draw an arc of radius 5.5 cm.
- With R as the centre, draw an arc of radius 5 cm.
- S is the point of intersection of the two arcs. Also, mark S and complete PQRS.
- PQRS is the required quadrilateral.
2. Construct a quadrilateral when two diagonals and three sides are given
Construct a quadrilateral ABCD, given that BC = 4.5 cm, AD = 5.5 cm, CD = 5 cm the diagonal AC = 5.5 cm and diagonal BD = 7 cm.
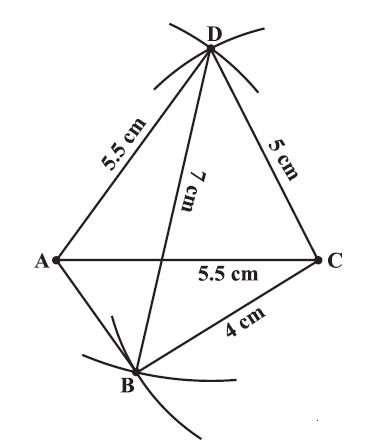
- Draw ACD using SSS construction.
- With D as centre, draw an arc of radius 7 cm.
- With C as centre, draw an arc of radius 4.5 cm
- Since B lies on both the arcs, B is the point intersection of the two arcs. Mark B and complete ABCD.
ABCD is the required quadrilateral
3. Construct a quadrilateral when two adjacent sides and three angles are given
Construct a quadrilateral ABCD, where sides adjacent sides AB & BC = 5 cm & 3 cm respectively. Also three angles the vertices A, B & C are 120 degree, 110 degree and 90 degree respectively.
Solution:
As per given question:
AB = 5 cm
BC = 3 cm
Angle A = 120 degree
Angle B = 110 degree
Angle C = 90 degree
Step of construction are as follows:
Step 1: Draw as line segment AB of 5 cm (as shown below)

Step 2: Use protractor and draw angle of 120 degree at vertex A (as shown below):
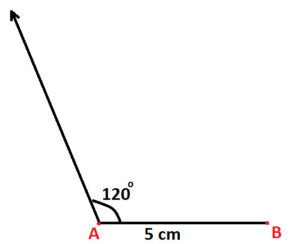
Step 3: Use protractor and draw angle of 110 degree at vertex B (as shown below):
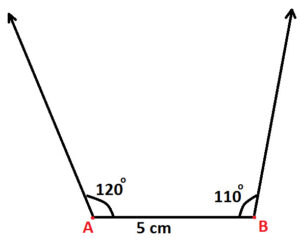
Step 4: Use compass and 3 cm wide open. With B as center, draw an arc with cuts the arm of 110 degree angle; drawn in step 3. And mark point of intersection as C (as shown below)
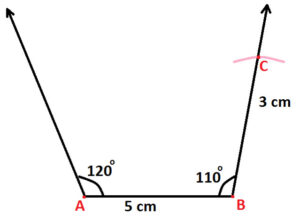
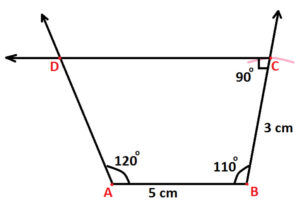
Step 5: Use protractor and draw angle of 90 degree at point C (as shown below):

Step 6: You can observe that arm of 90 degree angle cuts the arm of angle 120 degree angle. Mark point of this intersection as D. And we get resultant Quadrilateral ABCD (as shown below):
4. Construct quadrilaterals when three sides and two included angles are given.
Construct a quadrilateral ABCD, where sides adjacent sides AB, BC, AD = 5 cm, 3 cm & 4 cm respectively. Also two included angles - Angle A and Angle B are 120 degree & 110 degree respectively.
Solution: As per given question:
AB = 5 cm
BC = 3 cm
AD = 4 cm
Angle A = 120 degree
Angle B = 110 degree
Step of construction are as follows:
Step 1: Draw as line segment AB of 5 cm (as shown below)

Step 2: Use protractor and draw angle of 120 degree at vertex A (as shown below):

Step 3: Use compass and 4 cm wide open. With A as center, draw an arc with cuts the arm of 120 degree angle; drawn in step 4. And mark point of intersection as D (as shown below)

Step 4: Use protractor and draw angle of 110 degree at vertex B (as shown below):

Step 5: Use compass and 3 cm wide open. With B as center, draw an arc with cuts the arm of 110 degree angle; drawn in step 3. And mark point of intersection as C (as shown below)

Step 6: Join point C & D and we get the resultant quadrilateral ABCD (as shown below):
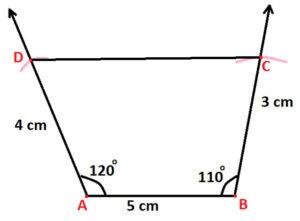
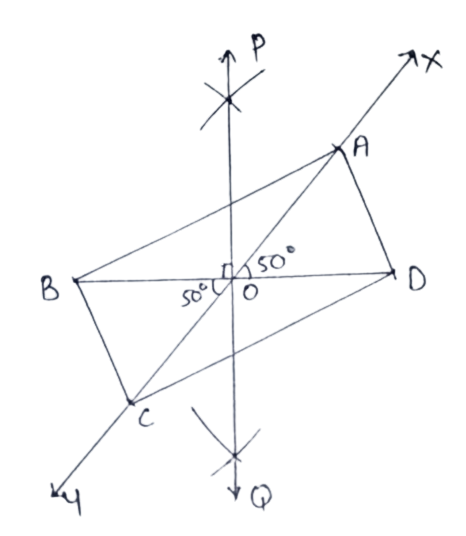
3. Construct a rectangle whose diagonal = 5.8 cm and angle between the diagonals is 50∘ .
Questions & Answers
Question 1: Quadrilateral ABCD
AB = 4.5 cm, BC = 5.5 cm, CD = 4 cm, AD = 6 cm, AC = 7 cm

Answer: Steps are as follows:
- Draw diagonal AC = 7 cm
- From point A, make an arc at 4.5 cm
- From point C, make an arc at 5.5 cm so that it intersects the previous arc. This is point B
- Join B to A and C to get AB and BC
- From point A, make an arc at 6 cm on another side of diagonal.
- From point C, make an arc at 4 cm so that it intersects the previous arc. This is point D.
- Join D to A and C to get AD and CD
- Quadrilateral ABCD is complete.
Question 2: Quadrilateral JUMP
JU = 3.5 cm, UM = 4 cm, MP = 5 cm, PJ = 4.5 cm, PU = 6.5 cm

Answer: Steps are as follows:
- Draw the diagonal PU = 6.5 cm
- From point P, make an arc at 4.5 cm
- From point U, make an arc at 3.4 cm so that it intersects the previous arc. This is point J
- Join J to P and U to get PJ and JU
- From point P, make an arc at 5 cm on another side of diagonal.
- Form point U, make an arc at 4 cm to intersect previous arc. This is point M
- Join M to P and U, to get PM and UM
- Quadrilateral JUMP is complete.
Question 3: Parallelogram MORE
OR = 6 cm, RE = 4.5 cm, EO = 7.5 cm

Answer: Steps are as follows:
- Draw diagonal EO = 7.5 cm
- From point O, make and arc at 6 cm.
- From point E, make an arc at 4.5 so that it intersects previous arc. This is point R.
- Join R to O and E to get OR and OE, and to get ΔROE
- From point E, make an arc at 6 cm on another side of diagonal.
- From point O, make an arc at 4.5 cm so that it intersects previous arc. This is point M.
- Join M to O and E to get OM and EM.
- Parallelogram MORE is complete.
Question 4: Rhombus BEST
BE = 4.5 cm, ET = 6 cm

Answer: We know that all sides of rhombus are equal.
- Draw ET = 6 cm
- From point E, make an arc at 4.5 cm
- From point T, make an arc at 4.5 cm so that it intersects previous arc. This is point B.
- Join B to E and T, to get BE and BT.
- From point E, make an arc at 4.5 cm on another side of diagonal
- From point T, make an arc at 4.5 cm so that it intersects previous arc. This is point S.
- Join S to E and T, to get SE and ST
- Rhombus BEST is complete.
Construct the following quadrilaterals
Question 1: Quadrilateral LIFT
LI = 4 cm, IF = 3cm, TL = 2.5 cm, LF = 4.5 cm, IT = 4 cm

Answer: Steps are as follows:
- Draw diagonal LF = 4.5 cm
- From point L, make and arc at 4 cm
- From point F, make an arc at 3 cm so that it intersects previous arc. This is point I
- Join I to L and F to get LI and IF
- From point L, make an arc at 2.5 cm on another side of diagonal.
- From point F, make an arc at 4 cm so that it intersects previous arc. This is point T.
- Join T to L and F to get TL and FT.
- Quadrilateral LIFT is complete.
Question 2: Quadrilateral GOLD
OL = 7.5 cm, GL = 4 cm, GD = 6 cm, LD = 5 cm, OD = 10 cm

Answer: Steps are as follows:
- Draw diagonal GL = 4 cm
- From point G, make an arc at 10 cm.
- From point L, make an arc at 7.5 cm so that it intersects previous arc. This is point O.
- Join O to G and L to get GO and OL
- From point G, make an arc at 6 cm, on another side of diagonal.
- Form point L, make an arc at 5 cm so that it intersects previous arc. This is point D.
- Join D to G and L to get DG and LD
- Quadrilateral GOLD is complete.
Question 3: Rhombus BEND
BN = 5.6 cm, DE = 6.5 cm

Answer: Diagonals of a rhombus are perpendicular bisectors of each other.
- Draw DE = 6.5 cm
- Draw the perpendicular bisector of DE, so that the bisector = BN = 5.6 cm
- Join four vertices to complete the rhombus BEND.
Question 1: Quadrilateral MORE
MO = 6 cm, OR = 4.5 cm, ∠M = 60°, ∠O = 105°, ∠R = 105°

Answer: Steps are as follows:
- Draw MO = 6 cm
- Make an angle = 105° at point O.
- Draw OR = 4.5 cm
- Make an angle = 105° at point R
- Make and angle = 60° at point M
- Extend lines from points M and R so that they intersect at point E.
- Quadrilateral MORE is complete.
Here, sum of given three angles of given quadrilateral is = 60 + 105 + 105 = 270
So, fourth angle = 360 – 270 = 90
Question 2: Quadrilateral PLAN
PL = 4 cm, LA = 6.5 cm, ∠P = 90°, ∠A = 110°, ∠N = 85°

Answer: Steps are as follows:
- Calculate fourth angle, i.e. ∠L = 360 – (90 + 110 + 85)
= 360 – 285 = 75 - Draw PL = 4 cm
- Make an angle of 90° on point P and another angle of 75° on point L.
- Draw LA = 6.5 cm
- Make an angle of 110° on point A
- Extend lines from P and A so that they intersect at point P
- Quadrilateral PLAN is complete.
Question 3: Parallelogram HEAR
HE = 5 cm, EA = 6 cm, ∠R = 85°

Answer: Steps are as follows:
- Draw HE = 5 cm
- Make an angle of 85° on point E
- Draw EA = 6 cm
- We know that adjacent angles are supplementary in a parallelogram.
- Supplement of 85° = 180° - 85° = 95°
- Make and angle of 95° on point A
- Draw AR = 5 cm so that it is parallel to HE
- Join H to R
- Parallelogram HEAR is complete.
Question 4: Rectangle OKAY
OK = 7 cm, KA = 5 cm

Answer: All angles of a rectangle are right angles and opposite sides are equal.
- Draw OK = 7 cm
- Draw KA = 5 cm perpendicular to OK
- Draw AY = 7 cm perpendicular to KA
- Join O to Y
- Rectangle OKAY is complete.
Construct the following quadrilaterals
Question 1: Quadrilateral DEAR
DE = 4 cm, EA = 5 cm, AR = 4.5 cm, ∠E = 60°, ∠A = 90°

Answer: Steps are as follows:
- Draw DE = 4 cm
- Make and angle of 60° on point E
- Draw EA = 5 cm
- Make a right angle at point A
- Draw AR = 4.5 cm
- Join D to R
- Quadrilateral DEAR is complete
Question 2: Quadrilateral TRUE
TR = 3.5 cm, RU = 3 cm, UE = 4 cm, ∠R = 75°, ∠U = 120°

Answer: Steps are as follows:
- Draw TR = 3.5 cm
- Make an angle of 75° on point R
- Draw RU = 3 cm
- Make an angle of 120° on point U
- Draw UE = 4 cm
- Join T to E
- Quadrilateral TRUE is complete
Draw the following
Question 1: The square READ with RE = 5.1 cm

Answer: All sides of a square are equal and all angles are right angle.
- Draw RE = 5.1 cm
- Draw EA = 5.1 cm perpendicular to RE
- Draw DA = 5.1 cm perpendicular to EA
- Join R to D
- Square READ is complete.
Question 2: A rhombus whose diagonals are 5.2 cm and 6.4 cm long

Answer: We know that diagonals of a rhombus are perpendicular bisectors of each other
- Draw a vertical line = 6.4 cm
- Draw the perpendicular bisector of this line of length 5.2 cm
- Join four vertices to complete the rhombus
Question 3: A rectangle with adjacent sides of lengths 5 cm and 4 cm

Answer: All angles of a rectangle are right angles and opposite sides are equal.
- Draw a horizontal line = 5 cm
- Draw another line which is perpendicular to previous line and its length = 4 cm
- Draw a third line which is perpendicular to second line with length = 5 cm
- Draw a fourth line which is perpendicular to third line.
- Rectangle is complete.
Question 4: A parallelogram OKAY where OK = 5.5 cm and KA = 4.2 cm. Is it unique?

Answer: Steps are as follows:
- Draw OK = 5.5 cm
- Draw KA = 4.5 cm at any angle
- Draw YA||OK
- Draw OY||KA
- Parallelogram is complete.
This is not a unique parallelogram, because different parallelograms can be made by changing the value of the angle between first two lines.

