Mensuration – Hari Shanker Pandey Sewa Samiti

KEY CONCEPTS

Learn concepts & fundamentals

Mensuration Formula of 2D Shapes

Square

Area (Square units) A = a x a = a²
Perimeter (units) P = sum of all sides = a+a+a+a = 4a

Rectangle

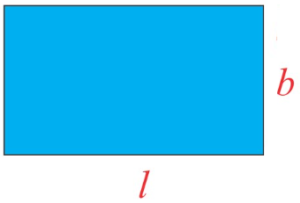
Area (Square units) A = l × b ,
Perimeter (units) P = sum of all sides = l+b+l+b = 2l+2b = 2(l+b)

Parallelogram

Area (Square units) A =base x height = b x h ,
Perimeter (units) P = sum of all sides = AB + BC + CD + DA

Trapezium

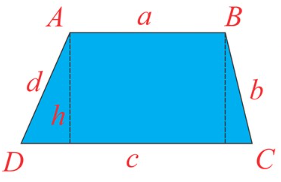
Area (Square units) A = $= \frac{1}{2} \times (a + c) \times h$
Perimeter (units) P = sum of all sides = a+b+c+d

Rhombus

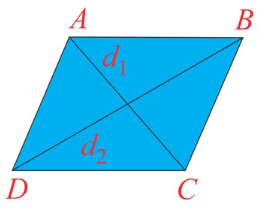
Area (Square units) A = $= \frac{1}{2} \times (a + c) \times h$ d₁ × d₂)
Perimeter (units) P = sum of all sides = 4 × side

Scalene Triangle

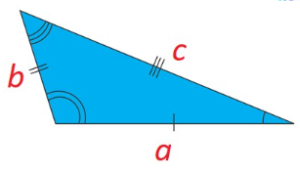
Area (Square units) A =√[s(s−a)(s−b)(s−c)], Where, s = (a+b+c)/2
Perimeter (units) P = sum of all sides = a+b+c

Equilateral Triangle

Area (Square units) A =(√3/4) × a²
Perimeter (units) P = sum of all sides = 3a

Isosceles Triangle

Area (Square units) A =½ × b × h
Perimeter (units) P = sum of all sides = 2a + b

Right-Angled Triangle

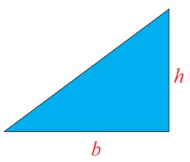
Area (Square units) A =½ × b × h
Perimeter (units) P = sum of all sides = b + hypotenuse + h

Circle

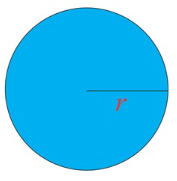
Area (Square units) A =πr²
Circumference or Perimeter (units) P = 2 π r

Semi Circle

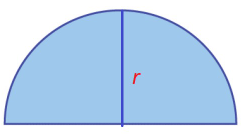
Area (Square units) A =½ πr²
Circumference or Perimeter (units) P = π r + 2 r

Mensuration Formula of 3D Shapes

Cube

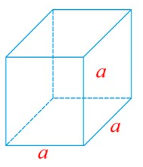
Volume (Cubic units) V = a³
Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units) = 4 a²
Total Surface Area (TSA) (Square units) = 6 a²

Cuboid

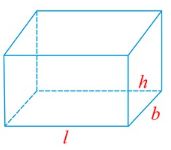
Volume (Cubic units) V = l × b × h
Curved Surface Area (CSA) or Lateral Surface Area (LSA) or Area of four walls of room (Square units) = 2h(l + b)
Total Surface Area (TSA) (Square units) = 2 (lb +bh +hl)

Cylinder

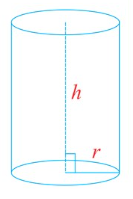
Volume (Cubic units) V = π r ² h
Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units) = 2π r h
Total Surface Area (TSA) (Square units) = 2πrh + 2πr²

Cone

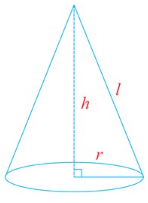
Volume (Cubic units) V = (⅓) π r² h
Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units) = π r l
Total Surface Area (TSA) (Square units) = πr (r + l)

Sphere

Volume (Cubic units) V = (4/3) π r³
Curved Surface Area (CSA) or Lateral Surface Area (LSA) (Square units) =4 π r²
Total Surface Area (TSA) (Square units) = 4 π r²

Questions & Answers

Question 1:

A square and a rectangular field with measurements as given in the figure have the same perimeter. Which field has a larger area?

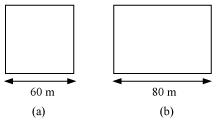
Ans: Perimeter of square = 4 (Side of the square) = 4 (60 m) = 240 m

Perimeter of rectangle = 2 (Length + Breadth)

= 2 (80 m + Breadth)

= 160 m + 2 × Breadth

It is given that the perimeter of the square and the rectangle are the same.

160 m + 2 × Breadth = 240 m

Breadth of the rectangle = = 40 m

Area of square = (Side)² = (60 m)² = 3600 m²

Area of rectangle = Length × Breadth = (80 × 40) m² = 3200 m²

Thus, the area of the square field is larger than the area of the rectangular field.

Question 2:

Mrs. Kaushik has a square plot with the measurement as shown in the following figure. She wants to construct a house in the middle of the plot. A garden is developed around the house. Find the total cost of developing a garden around the house at the rate of Rs 55 per m².

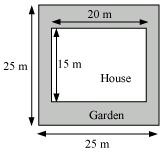
Ans:

Area of the square plot = (25 m)² = 625 m²

Area of the house = (15 m) × (20 m) =300 m²

Area of the remaining portion = Area of square plot − Area of the house

= 625 m² − 300 m² = 325 m²

The cost of developing the garden around the house is Rs 55 per m².

Total cost of developing the garden of area 325 m² = Rs (55 × 325)

= Rs 17,875

Question 3:

The shape of a garden is rectangular in the middle and semi circular at the ends as shown in the diagram. Find the area and the perimeter of the garden [Length of rectangle is 20 − (3.5 + 3.5) metres]

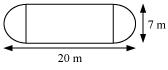
Ans:

Length of the rectangle = [20 − (3.5 + 3.5)] metres = 13 m

Circumference of 1 semi-circular part = πr

Circumference of both semi-circular parts = (2 × 11) m = 22 m

Perimeter of the garden = AB + Length of both semi-circular regions BC and

DA + CD

= 13 m + 22 m + 13 m = 48 m

Area of the garden = Area of rectangle + 2 × Area of semi-circular region

Question 4:

A flooring tile has the shape of a parallelogram whose base is 24 cm and the corresponding height is 10 cm. How many such tiles are required to cover a floor of area 1080 m²? (If required you can split the tiles in whatever way you want to fill up the corners).

Ans: Area of parallelogram = Base × Height

Hence, area of one tile = 24 cm × 10 cm = 240 cm²

Required number of tiles =

= 45000 tiles

Thus, 45000 tiles are required to cover a floor of area 1080 m².

Question 5:

An ant is moving around a few food pieces of different shapes scattered on the floor. For which food − piece would the ant have to take a longer round? Remember, circumference of a circle can be obtained by using the expression c = 2πr, where r is the radius of the circle.

Ans: (a)Radius (r) of semi-circular part =

Perimeter of the given figure = 2.8 cm + πr

(b)Radius (r) of semi-circular part =

Perimeter of the given figure = 1.5 cm + 2.8 cm + 1.5 cm +π (1.4 cm)

(c)Radius (r) of semi-circular part =

Perimeter of the figure(c) = 2 cm + πr + 2 cm

Thus, the ant will have to take a longer round for the food-piece (b), because the perimeter of the figure given in alternative (b) is the greatest among all.

Question 6:

The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and perpendicular distance between them is 0.8 m.

Ans: Area of trapezium = (Sum of parallel sides) × (Distances between parallel sides)

Question 7:

The area of a trapezium is 34 cm² and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

Ans: It is given that,area of trapezium = 34 cm² and height = 4 cm

Let the length of one parallel side be a. We know that,

Area of trapezium = (Sum of parallel sides) × (Distances between parallel sides)

Thus, the length of the other parallel side is 7 cm.

Question 8:

Length of the fence of a trapezium shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Ans: Length of the fence of trapezium ABCD = AB + BC + CD + DA

120 m = AB + 48 m + 17 m + 40 m

AB = 120 m − 105 m = 15 m

Area of the field ABCD

Question 9:

The diagonal of a quadrilateral shaped field is 24 m and the perpendiculars dropped on it from the remaining opposite vertices are 8 m and 13 m. Find the area of the field.

Ans: It is given that,

Length of the diagonal, d = 24 m

Length of the perpendiculars, h₁ and h₂, from the opposite vertices to the diagonal are h₁ = 8 m and h₂ = 13 m

Area of the quadrilateral

Thus, the area of the field is 252 m².

Question 10:

The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.

Ans: Area of rhombus = (Product of its diagonals)

Therefore, area of the given rhombus

= 45 cm²

Question 11:

Find the area of a rhombus whose side is 5 cm and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.

Ans: Let the length of the other diagonal of the rhombus be x.

A rhombus is a special case of a parallelogram.

The area of a parallelogram is given by the product of its base and height.

Thus, area of the given rhombus = Base × Height = 5 cm × 4.8 cm = 24 cm²

Also, area of rhombus = (Product of its diagonals)

Thus, the length of the other diagonal of the rhombus is 6 cm.

Question 12:

Mohan wants to buy a trapezium shaped field. Its side along the river is parallel to and twice the side along the road. It the area of this field is 10500 m² and the perpendicular distance between the two parallel sides is 100 m, find the length of the side along the river.

Ans: Let the length of the field along the road be l m. Hence, the length of the field along the river will be 2l m.

Area of trapezium = (Sum of parallel sides) (Distance between the parallel sides)

Thus, length of the field along the river = (2 × 70) m = 140 m

Question 13:

If each edge of a cube is doubled,

(i) how many times will its surface area increase?

(ii) how many times will its volume increase?

Ans: (i) Let initially the edge of the cube be l.

Initial surface area = 6l²

If each edge of the cube is doubled, then it becomes 2l.

New surface area = 6(2l)² = 24l² = 4 × 6l²

Clearly, the surface area will be increased by 4 times.

(ii) Initial volume of the cube = l³

When each edge of the cube is doubled, it becomes 2l.

New volume = (2l)³ = 8l³= 8 × l³

Clearly, the volume of the cube will be increased by 8 times.

Question 14:

Water is pouring into a cubiodal reservoir at the rate of 60 litres per minute. If the volume of reservoir is 108 m³, find the number of hours it will take to fill the reservoir.

Ans: Volume of cuboidal reservoir = 108 m³ = (108 × 1000) L = 108000 L

It is given that water is being poured at the rate of 60 L per minute.

That is, (60 × 60) L = 3600 L per hour

Required number of hours = 30 hours

Thus, it will take 30 hours to fill the reservoir.

Question 15:

A milk tank is in the form of cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in litres that can be stored in the tank?

Ans:

Radius of cylinder = 1.5 m

Length of cylinder = 7 m

Volume of cylinder

1m³ = 1000 L

Required quantity = (49.5 × 1000) L = 49500 L

Therefore, 49500 L of milk can be stored in the tank.

Question 16:

Find the height of a cuboid whose base area is 180 cm² and volume is 900 cm³?

Ans: Base area of the cuboid = Length × Breadth = 180 cm²

Volume of cuboid = Length × Breadth × Height

900 cm³ = 180 cm² × Height

Thus, the height of the cuboid is 5 cm.

Question 17:

Diameter of cylinder A is 7 cm, and the height is 14 cm. Diameter of cylinder B is 14 cm and height is 7 cm. Without doing any calculations can you suggest whose volume is greater? Verify it by finding the volume of both the cylinders. Check whether the cylinder with greater volume also has greater surface area?

Ans: The heights and diameters of these cylinders A and B are interchanged.

We know that,

Volume of cylinder

If measures of r and h are same, then the cylinder with greater radius will have greater area.

Radius of cylinder A = cm

Radius of cylinder B = cm = 7 cm

As the radius of cylinder B is greater, therefore, the volume of cylinder B will be greater.

Let us verify it by calculating the volume of both the cylinders.

Volume of cylinder A

Volume of cylinder B

Volume of cylinder B is greater.

Surface area of cylinder A

Surface area of cylinder B

Thus, the surface area of cylinder B is also greater than the surface area of cylinder A.

Question 18:

Given a cylindrical tank, in which situation will you find surface area and in which situation volume.

(a) To find how much it can hold

(b) Number of cement bags required to plaster it

ANSWER:

(a) In this situation, we will find the volume.

(b) In this situation, we will find the surface area.

Mock Test

Test your knowledge

Name

Mobile

The length and breadth of a rectangular field are in the ratio 9 : 5. If the area of the field is 14580 square metres, find the cost of surrounding the field with a fence at the rate of ₹3.25 per metre.

If each edge of a cube is tripled, then find how many times will its volume become?

In a class of 30 pupils, 12 take needle work, 16 take physics and 18 take history. If all the 30 students take at least one subject and no one takes all three then the number of pupils taking 2 subjects is

A closed box is made of 2 cm thick wood with external dimension 84 cm × 75 cm × 64 cm. Find the volume of the wood required to make the box.

If two sets A and B are having 99 elements in common, then the number of elements common to each of the sets A×B and B×A are

A milk tank is in the form of cylinder whose radius is 1.4 m and height is 8 m. Find the quantity of milk in litres that can be stored in the tankand B are subsets of U, then n((A∪B)C)=

Two cylindrical jars contain the same amount of milk. If their diameters are in the ratio 3 : 4, find the ratio of their heights.

A rectangular piece of tin of size 30 cm × 18 cm is rolled in two ways, once along its length (30 cm) and once along its breadth. Find the ratio of volumes of two cylinders so formed.

Two cylindrical vessels are filled with milk. The radius of one vessel is 15 cm and height is 40 cm, and the radius of other vessel is 20 cm and height is 45 cm. Find the radius of another cylindrical vessel of height 30 cm which may just contain the milk which is in the two given vessels.

Find the total surface area of a solid cylinder of radius 5 cm and height 10 cm. Leave your answer in terms of n.

The curved surface area of a hollow cylinder is 4375 cm2, it is cut along its height and formed a rectangular sheet of width 35 cm. Find the perimeter of the rectangular sheet.

A rectangular paper is size 22 cm × 14 cm is rolled to form a cylinder of height 14 cm, find the volume of the cylinder. (Take π = 22/7)

The inner dimensions of a closed wooden box are 2 m by 1.2 m by 0.75 m. The thickness of the wood is 2.5 cm. Find the cost of wood required to make the box if 1 m3 of wood costs ₹5400.