Concepts
When two triangles are congruent they will have exactly the same three sides and exactly the same three angles.
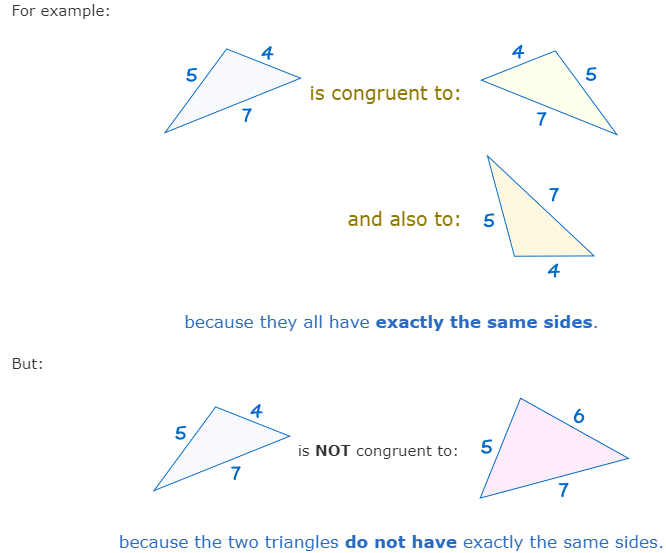
How To Find if Triangles are Congruent?
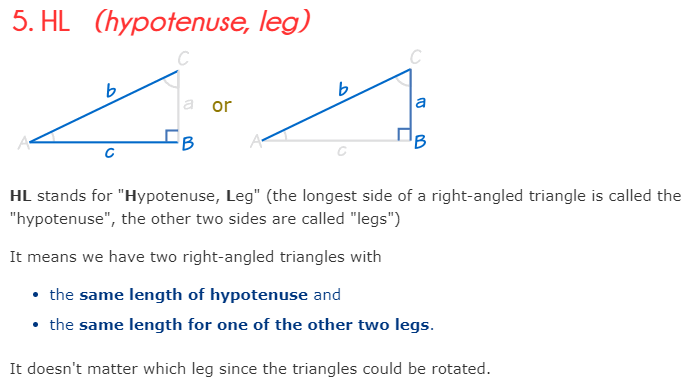
There are five ways to find if two triangles are congruent: SSS, SAS, ASA, AAS and HL.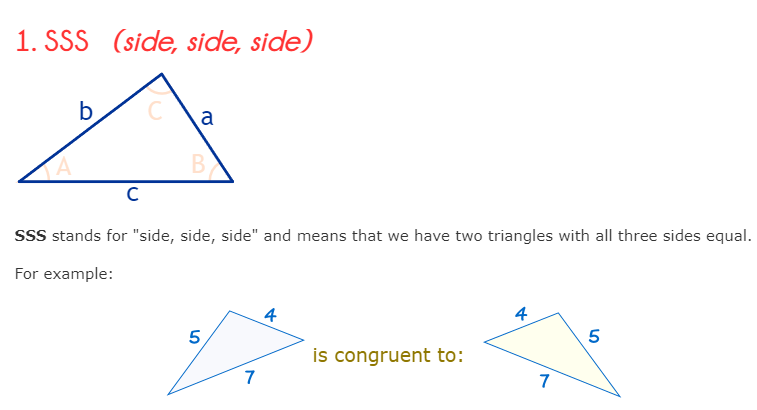
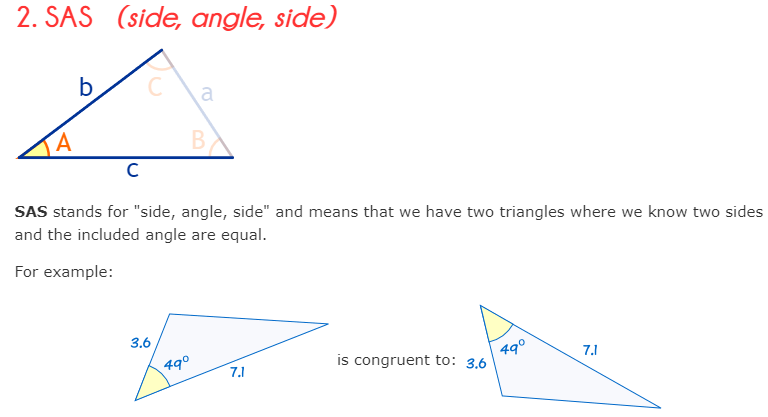
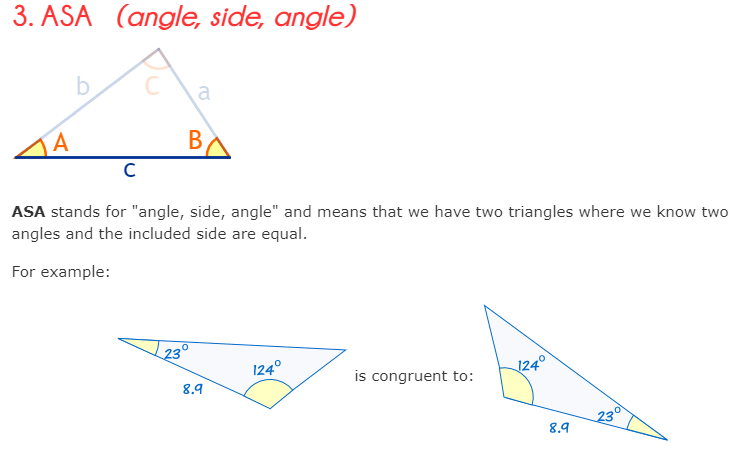

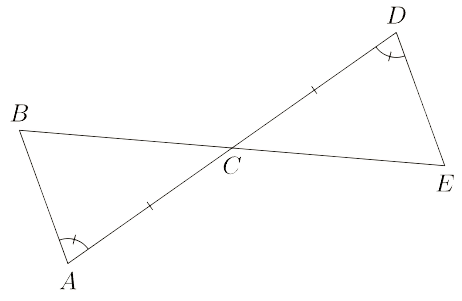
CPCTC stands for "corresponding parts of congruent triangles are congruent" and tells us if two or more triangles are congruent, then their corresponding angles and sides are congruent as well.
Questions & Answers
Example 1: In the following figure, AB = BC and AD = CD. Show that BD bisects AC at right angles.
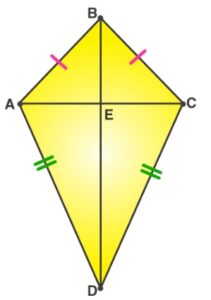
Solution: We are required to prove ∠BEA = ∠BEC = 90° and AE = EC.
Consider ∆ABD and ∆CBD, AB = BC (Given)AD = CD (Given)BD = BD(Common)
Therefore, ∆ABD ≅ ∆CBD (By SSS congruency)
∠ABD = ∠CBD (CPCTC)
Now, consider ∆ABE and ∆CBE,
AB = BC (Given)
∠ABD = ∠CBD (Proved above)
BE = BE (Common)
Therefore, ∆ABE≅ ∆CBE (By SAS congruency)
∠BEA = ∠BEC (CPCTC)
And ∠BEA +∠BEC = 180° (Linear pair)
2∠BEA = 180° (∠BEA = ∠BEC)
∠BEA = 180°/2 = 90° = ∠BEC
AE = EC (CPCTC)
Hence, BD is a perpendicular bisector of AC.
Example 2: In a Δ ABC, if AB = AC and ∠ B = 70°, find ∠ A.
Solution: Given: In a Δ ABC, AB = AC and ∠B = 70°
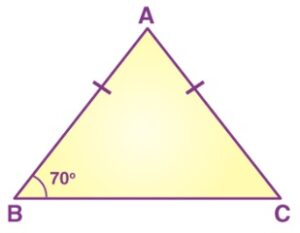
∠ B = ∠ C [Angles opposite to equal sides of a triangle are equal]
Therefore, ∠ B = ∠ C = 70°
Sum of angles in a triangle = 180°
∠ A + ∠ B + ∠ C = 180°
∠ A + 70° + 70° = 180°
∠ A = 180° – 140°
∠ A = 40°
Example 3: Prove that the opposite angles of a parallelogram are equal.
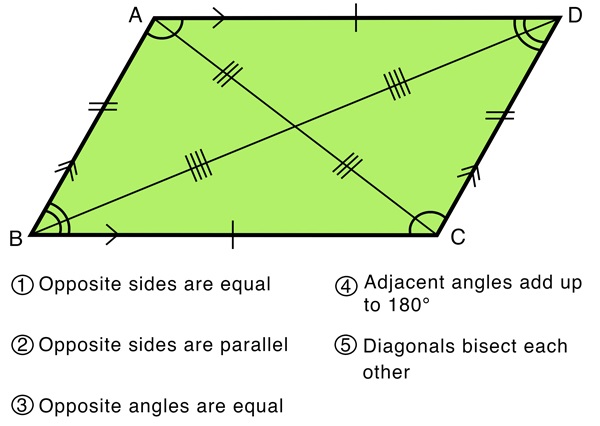
Δ ABC =Δ ADC ( Rule SSS)
AC is common for both Δ
Therefore, ∠ ABC = ∠ ADC
Parallelogram ABCD. We know that alternate interior angles are equal. By ASA congruence criterion, two triangles are congruent to each other. Hence, it is proved that the opposite angles of a parallelogram are equal.
Example 4: Prove that the diagonals of a parallelogram bisect each other.

Let ABCD be the parallelogram. Therefore, AB || DC and AD||BC.
Consider triangle AOD and COB.
AD = BC (opposite sides of a parallelogram)
∠DAO = ∠BCO (Alterante angles)
∠ADO = ∠CBO (Alternate angles)
Therefore, by ASA congruency, the triangle are congruent.
Now AO = OC and BO = OD because they are corresponding sides of two congruent triangle. Thus, the diagonals of a parallelogram bisect each other.
Example 4: Prove that the diagonals of a rectangle are equal.
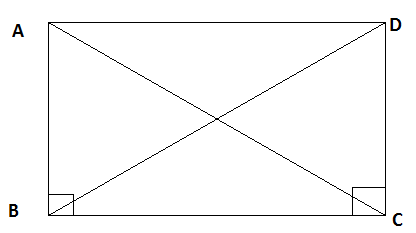
A rectangle is a parallelogram with opposite sides equal and the measure of each angle is 90∘
In above rectangle, consider rectangles ABC and DCB.
∠ABC=∠DCB=90∘ [Angles of rectangle]
BC=BC (common side)
AB=DC (Opposite sides of a parallelogram are equal)
Hence, △ABC≅△DCB.
AC=DB [CPCT]
Hence the diagonals of a rectangle are equal.

