Definition :

• A CIRCLE is the locus of a point which moves in a plane in such a way that its distance from a given fixed point in the plane is always constant.
• Any closed shape with all points connected at equidistance from centre forms a Circle.

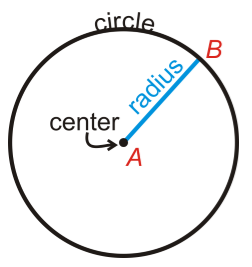
Here AB is Radius=r =d/2, where d is diameter of circle.

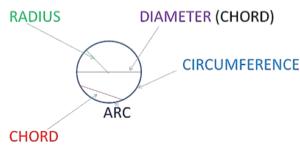
• Chord: Any straight line segment that’s both endpoints falls on the boundary of the circle is known as Chord. In Latin, it means ‘bowstring’.
• Diameter: Any straight line segment or Chord which passes through the centre of the Circle and its endpoints connects on the boundary of the Circle is known as the Diameter of Circle. So in a circle Diameter is the longest chord possible in a circle.
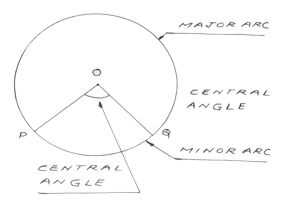
• Arc: Any smooth curve joining two points is known as Arc. So in Circle, we can have two possible Arcs, the bigger one is known as Major Arc and the smaller one is known as Minor Arc.
• Circumference: It is the length of the circle if we open and straightened out to make a line segment.
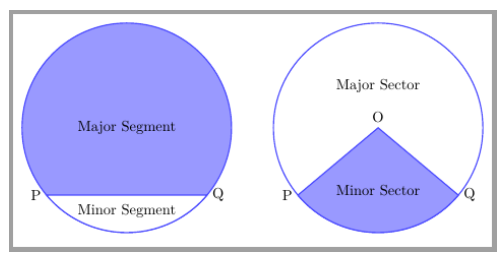
• A segment of the circle is the region between either of its arcs and a chord. It could be a major or minor segment.
• Sector of the circle is the area covered by an arc and two radii joining the centre of the circle. It could be the major or minor sector.

Angle Subtended by a Chord at a Point
If in a circle AB is the chord and is making ∠ACB at any point of the circle then this is the angle subtended by the chord AB at a point C.

Likewise, ∠AOB is the angle subtended by chord AB at point O i.e. at the centre and ∠ADB is also the angle subtended by AB at point D on the circle.

ARC OF A CIRCLE : P1P2 is an ARC

CENTRAL ANGLE

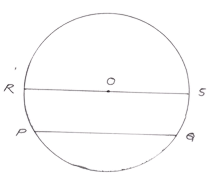
CHORD & DIAMETER : PQ is a CHORD, RS is a DIAMETER

SEGMENT OF A CIRCLE 

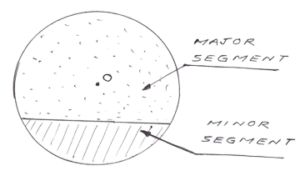
The major and minor segments of a circle are called the alternate segments of each other.

CONGRUENCE OF CIRCLES AND ARCS :

• Theorem 1 : If two arcs of a circle ( or of congruent circles ) are congruent, then corresponding chords are equal.

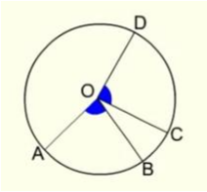
• Theorem 2 : If two chords of a circle ( or of congruent circles ) are equal, then their corresponding arcs ( minor, major or semi-circular ) are congruent .
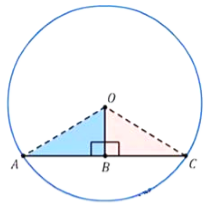
• Theorem 3 : The perpendicular from the centre of a circle to a chord bisects the chord..

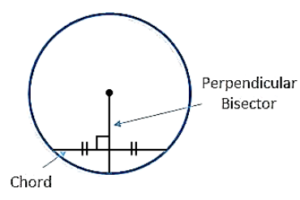
• Theorem 4 : The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.

• Theorem 5 : There is one and only one circle passing through three non collinear points.

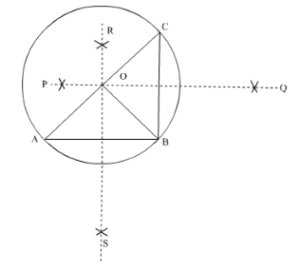
• Theorem 6 : Two chords AB and AC of a circle are equal. Then centre of the circle lies on the angle bisectors of angle ABC.
• Theorem 7 : If two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of angle BAC, than AB = AC i.e. the chords are equal.
• Theorem 8 : If two circles intersects in two points, then the line through the centres is the perpendicular bisector of the common chord.

RESULTS ON EQUAL CHORDS:

• Theorem 1 : Any two equal chords of a circle subtend equal angles at the centre.

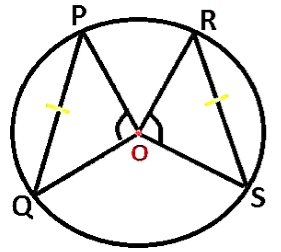
• Theorem 2 : If the angles made by the chords of a circle at the centre are equal, then the chords must be equal.This theorem is the reverse of the above Theorem 1.
• Theorem 3 : Equal chords of congruent circles are equidistant from the corresponding centres.
• Theorem 4 : Chords of congruent circles which are equidistant from the corresponding centres are equal.
• Theorem 5 : Equal chords of a circle subtend equal angles at the centre.This is the reverse of the below theorem which says that if the distance between the centre and the chords are equal then they must be of equal length.
• Theorem 6 : If the angle subtended by two chords of a circle at the centre are equal, then chords are equal.

AB and CD are the two equal chords in the circle. If we draw the perpendicular bisector of these chords then the line segment from the centre to the chord is the distance of the chord from the centre.If the chords are of equal size then their distance from the centre will also be equal.

• Theorem 7 : Equal chords of congruent circles subtend equal angles at the centre.
• Theorem 8 : If the angles subtended by the two chords of congruent circles at the corresponding centres are equal, then chords are equal.
• Theorem 9 : Of any two chords of a circle, the one which is larger is nearer to the centre.
• Theorem 10 : Of any two chords of a circle, the one which is nearer to the centre is larger.

ARCS AND ANGLES SUBTENDED BY THEM

• Theorem 1 : The angle subtended by any arc of a circle at the centre is double the angle subtended by it at any point on the remainder part of the circle.
  Angle A = 2 x Angle B

• Theorem 2 : Angles in the same segment of a circle are equal i.e. Angle R = Angle S

• Theorem 3 : The angle in a semi-circle is a right angle.
• Theorem 4 : The arc of a circle subtending a right angle at any point of the circle in its alternate segment is a semi-circle.
• Theorem 5 : Any angle subtended by a minor arc in the alternate segment is acute and any angle subtended by a major are in the alternate segment is obtuse i.e.
  Angle R = Acute and Angle S = Obtuse

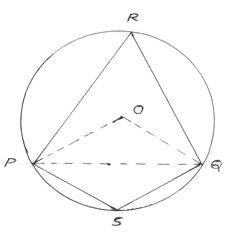
• Theorem 6 : If a line segment joining two points subtends equal angles at two other points lying on the same side of the line segment, then four points are concyclic i.e. lie on the same circle.

CYCLIC QUADRILATERAL:
A quadrilateral is said to be cyclic if it’s all vertices lie on a circle.

∠A + ∠B + ∠C + ∠D = 360º (angle sum property of a quadrilateral)

∠A + ∠C = 180°

∠B + ∠D = 180º

• Theorem 1 : The opposite angles of a cyclic quadrilateral are supplementary.
• Theorem 2 : If the sum of any pair of opposite angles of a quadrilateral is 180º, then the quadrilateral is cyclic.
• Theorem 3 : If one side of a cyclic quadrilateral is produced, then the exterior angles are equal to the interior opposite angles i.e. Angle CBE = Angle D
• Theorem 4 : The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic i.e. Quad PQRS is Cyclic.

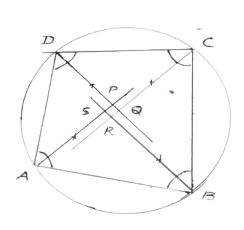
• Theorem 5 : If two sides of acyclic quadrilateral are parallel, then remaining two sides are equal and the diagonals are also equal i.e. if DC is parallel to AB, then AD = BC and also AC = BD.

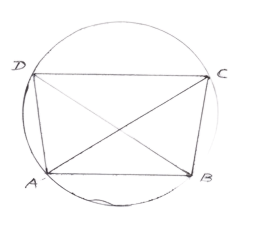
• Theorem 6 : If two opposite sides of acyclic quadrilateral are equal, then other two sides are parallel i.e. if AD = BC then AB is parallel to CD.

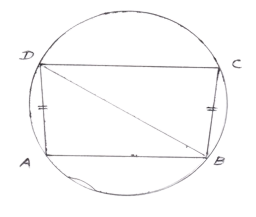
• Theorem 7 : If two non-parallel sides of a trapezium are equal, it is cyclic.
• Theorem 8 : If the bisectors of the opposite angles Angle P and Angle R of a cyclic quadrilateral PQRS intersect the corresponding circle at A and B respectively, then AB is a diameter of the circle i.e. AB is a diameter.

• Theorem 9 : The sum of angles in the four segment exterior to acyclic quadrilateral is equal to 6 right angles i.e. Angle P + Angle Q + Angle R + Angle S = 6 x 900