Key Concept
- An Arithmetic Progression is a sequence of numbers in which we get each term by adding a particular number to the previous term, except the first term.
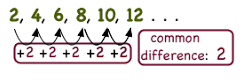
- Each number in the sequence is known as term.
- The fixed number i.e. the difference between each term with its preceding term is known as common difference. It can be positive, negative or zero. It is represented as ‘d’.
- Some Examples of Arithmetic Progressions
Common difference Value of d Example d > 0, positive 10 20, 30, 40, 50,… d < 0, negative -25 100, 75, 50, 25, 0 d = 0, zero 0 5, 5, 5, 5,.. -
General form of Arithmetic Progression

Where the first term is ‘a’ and the common difference is ‘d’.
Example
Given sequence is 2, 5, 8, 11, 14,…
Here, a = 2 and d = 3
d = 5 – 2 = 8 – 5 = 11 – 8 = 3
First term is a = 2
Second term is a + d = 2 + 3 = 5
Third term is a + 2d = 2 + 6 = 8 and so on.
Finite or Infinite Arithmetic Progressions
1. Finite Arithmetic Progression
If there are only a limited number of terms in the sequence then it is known as finite Arithmetic Progression.
229, 329, 429, 529, 629
2. Infinite Arithmetic Progression
If there are an infinite number of terms in the sequence then it is known as infinite Arithmetic Progression.
2, 4, 6, 8, 10, 12, 14, 16, 18…..…
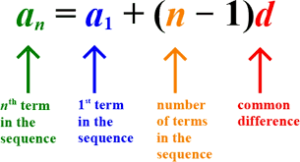
The nth term of an Arithmetic Progression
If an is the nth term,a1 is the first term, n is the number of terms in the sequence and d is a common difference then the nth term of an Arithmetic Progression will be
Example
Find the 11th term of the AP: 24, 20, 16,…
Solution
Given a = 24, n = 11, d = 20 – 24 = – 4
an = a + (n - 1)d
a11 = 24 + (11-1) – 4
= 24 + (10) – 4
=24 – 40
= -16
Arithmetic Series
The arithmetic series is the sum of all the terms of the arithmetic sequence.
The arithmetic series is in the form of
{a + (a + d) + (a + 2d) + (a + 3d) + .........}
Sum of first n terms of an Arithmetic series
Sum of the first n terms of the sequence is calculated by
Example
If Radha save some money every month in her piggy bank, then how much money will be there in her piggy bank after 12 months, if the money is in the sequence of 100, 150, 200, 250, ….respectively?
Solution
Given sequence is-
100, 150, 200, 250, …
a = 100 (first term)
d = 50 (common difference)
n = 12 (as we have to calculate money of 12 months)
Now we will put the values in the formula

So the money collected in her bank in 12 months is Rs. 4500.
But when we have finite Arithmetic Progression or we know the last term of the sequence then the sum of all the given terms of the progression will be calculated by
Where l = a + (n – 1)d i.e. the last term of the finite Arithmetic Progression.
Remark: The sum of the infinite arithmetic sequence does not exist.
Example
Find the sum of the sequence 38, 36, 34, 32, 30.
Solution
Given

Geometric Progression
A Geometric Progression is a sequence of numbers in which we get each term by multiplying or dividing a particular number to the previous term, except the first term.
The ratio between every term to the next term is constant.

nth term of the Geometric Sequence
an = a1 r n - 1
Sum of Geometric Series

Harmonic Progression
It is the reverse of Arithmetic Progression. If a, a + d, a + 2d …..is an Arithmetic Progression then the harmonic progression is

nth term of Harmonic Progression

Remark: There is no special formula for finding the sum of the harmonic series so we can calculate the sum of the arithmetic series and then take the reciprocal of it which will be the sum of the harmonic series.
The harmonic series is divergent to infinity.
Arithmetic Mean
Arithmetic mean is the average of the two numbers. If a, b and c are in Arithmetic Progression then the arithmetic mean of a and c will be

Some Important Points
- Sum of first n positive integers is given by

- The difference between the sum of the first n terms and first (n - 1) terms is also the nth term of the given Arithmetic Progression.
an = Sn – Sn-1
Geometric Mean
Geometric mean is the average of two numbers. If a and b are the two numbers then the geometric mean will be

Relationship between A.M. and G.M.
As we have seen above the formula for the Arithmetic mean and the Geometric mean are as follows-


Where a and b are the two given positive numbers.
Let A and G be A.M. and G.M.
So

Now let’s subtract the two means with each other

This shows that A ≥ G
Properties of relationship of A.M and G.M.
Property I: If the Arithmetic Mean and Geometric Mean of two positive numbers a and b are A and G respectively, then
A > G
As A – G > 0
Property II: If A be the Arithmetic Mean and G be the Geometric Mean between two positive numbers a and b, then the quadratic equation whose roots are a, b is
x2 - 2Ax + G2 = 0
Property III: If A is the Arithmetic Means and G be the Geometric Means between two positive numbers, and then the numbers are
A ± √A2 – G2
Harmonic Mean
Harmonic mean is calculated by dividing the number of items with the sum of the reciprocals of all the items.

Harmonic mean is used when there are extreme observations. Like

In this case if we will use arithmetic mean to find the average then we will get the inaccurate average.
Relation between AM, GM and HM
If a and b are two positive real numbers then

AM ≥ GM

GM ≥ HM
The combination of above two inequalities shows that
AM ≥ GM ≥ HM

