An algebraic expression (or) a variable expression is a combination of terms by the operations such as addition, subtraction, multiplication, division, etc. For example, let us have a look at the expression 5x + 7. Thus, we can say that 5x + 7 is an example of an algebraic expression. Here are more examples:
- 5x + 4y + 10
- 2x2y - 3xy2
- (-a + 4b)2 + 6ab
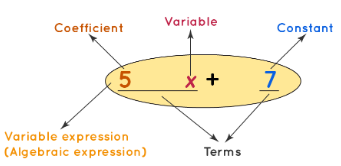
- In a polynomial, degree is the highest power of the variable.
Types of Algebraic expression
There are 3 main types of algebraic expressions which include:
- Monomial Expression
- Binomial Expression
- Polynomial Expression
Monomial Expression
An algebraic expression which is having only one term is known as a monomial.
Examples of monomial expressions include 3x4, 3xy, 3x, 8y, etc.
Binomial Expression
A binomial expression is an algebraic expression which is having two terms, which are unlike.
Examples of binomial include 5xy + 8, xyz + x3, etc.
Polynomial Expression
In general, an expression with more than one term with non-negative integral exponents of a variable is known as a polynomial.
Examples of polynomial expression include ax + by + ca, x3 + 2x + 3, etc.
Other Types of Expression
Apart from monomial, binomial and polynomial types of expressions, an algebraic expression can also be classified into two additional types which are:
- Numeric Expression
- Variable Expression
Numeric Expression
A numeric expression consists of numbers and operations, but never include any variable. Some of the examples of numeric expressions are 10 + 5, 15 ÷ 2, etc.
Variable Expression
A variable expression is an expression that contains variables along with numbers and operation to define an expression. A few examples of a variable expression include 4x + y, 5ab + 33, etc.
Example: Simplify the given expressions by combining the like terms and write the type of Algebraic expression.
(i) 3xy3 + 9x2 y3 + 5y3x
(ii) 7ab2 c2 + 2a3 b2 − 3abc – 5ab2 c2 – 2b2 a3 + 2ab
(iii) 50x3 – 20x + 8x + 21x3 – 3x + 15x – 41x3
Solution:
Creating a table to find the solution:
| S.no | Term | Simplification | Type of Expression |
|---|---|---|---|
| 1 | 3xy3 + 9x2 y3 + 5y3x | 8xy3 + 9x2y3 | Binomial |
| 2 | 7ab2 c2 + 2a3 b2 − 3abc – 5ab2 c2 – 2b2 a3 + 2ab | 2ab2 c2 − 3abc + 2ab | Trinomial |
| 3 | 50x3 – 20x + 8x + 21x3 – 3x + 15x – 41x3 | 30x³ | Monomial |
Formulas
The general algebraic formulas we use to solve the expressions or equations are:
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- a2 – b2 = (a – b)(a + b)
- (a + b)3 = a3 + b3 + 3ab(a + b)
- (a – b)3 = a3 – b3 – 3ab(a – b)
- a3 – b3 = (a – b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 – ab + b2)
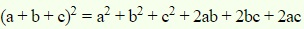
- an x am = an+m
- an / am = an-m
Sign conversions
If a * b = c, then
- (+ a) (+ b) = + c
- (– a) (– b) = + c
- ( – a) (b) = – c
- (+ a) (– b) = – c
Speed of the Train = Total distance covered by the train / Time taken
- If the length of two trains is given, say a and b, and the trains are moving in opposite directions with speeds of x and y respectively, then the time taken by trains to cross each other = {(a+b) / (x+y)}
- If the length of two trains is given, say a and b, and they are moving in the same direction, with speeds x and y respectively, then the time is taken to cross each other = {(a+b) / (x-y)}
Degree of a constant polynomial is ___________
Answer: 0. A polynomial having no variables and only constant values is called a constant polynomial.
For example.- f(x)=8,g(k)=−10. ∴ A constant polynomial has its highest degree as 0.
Write the degree of the following polynomial.
Solution
Verify whether the following expression is a polynomial?
State whether the following expression is polynomial or not. In case of a polynomial, write its degree.
Which of the following expression is a polynomial
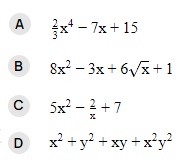
Solution
Clearly, only A is a polynomial, because a polynomial is a single variable equation and does not contain fractional or irrational term in variable x.
The product of two factors with unlike signs is............
Answer: The product of two factors with unlike signs is negative. Since, product of + and − is always −.
e.g. −3×2=−6
Answer:
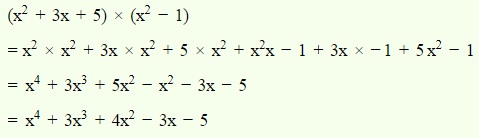
Evaluate using suitable standard identity.
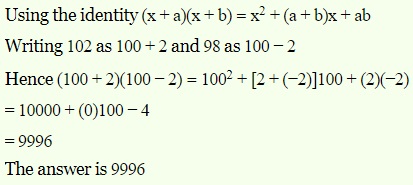
Similarly find the value of 10.2 x9.8 )
Answer: We can write above value as ( 9.8 + 0.2 ) ( 9.8 - 0.2 ).
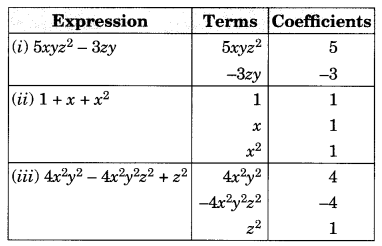
Identify the terms, their coefficients for each of the following expressions.
(i) 5xyz2 – 3zy
(ii) 1 + x + x2
(iii) 4x2y2 – 4x2y2z2 + z2
(iv) 3 – pq + qr – rp
(v) x/2 + y/2 – xy
(vi) 0.3a – 0.6ab + 0.5b
Solution:
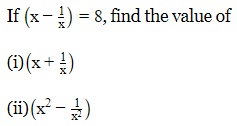
Hint: Use the following tricks to solve the problem:
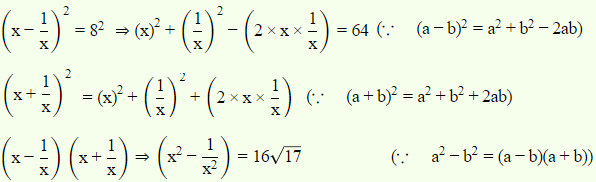
Divide: 6x3y2z2 by 3x2yz
Solution:
We have,
6x3y2z2 / 3x2yz
By using the formula an / am = an-m
6/3 x3-2 y2-1 z2-1
2xyz
Divide: x + 2x2 + 3x4 – x5 by 2x
Solution:
We have,
(x + 2x2 + 3x4 – x5) / 2x
x/2x + 2x2/2x + 3x4/2x – x5/2x
By using the formula an / am = an-m
1/2 x1-1 + x2-1 + 3/2 x4-1 – 1/2 x5-1
1/2 + x + 3/2 x3 – 1/2 x4
Divide: x2 + 7x + 12 by x + 4
Solution:
