Concepts
Square Root : The square root of a number is the inverse operation of squaring a number.If 'a' is the square root of 'b', it means that a × a = b.
22 = 4, so the square root of 4 is 2
102 = 100, therefore square root of 100 is 10
There are two square roots of any number. One is positive and other is negative.
The square root of 100 could be 10 or -10.
Symbol of Positive Square Root

We can use four methods to find the square root of numbers and those methods are as follows:
- Repeated Subtraction Method
- Prime Factorization Method
- Estimation Method
- Long Division Method
Repeated Subtraction Method of Square Root
This is a very simple method. We subtract the consecutive odd numbers from the number for which we are finding the square root, till we reach 0. The number of times we subtract is the square root of the given number. This method works only for perfect square numbers. Let us find the square root of 16 using this method.
- 16 - 1 = 15
- 15 - 3 =12
- 12 - 5 = 7
- 7- 7 = 0
You can observe that we have subtracted 4 times. Thus,√16 = 4
Example : Calculate the square root of 64 by repeated addition.
Solution:
64 – 1 = 63
63 – 3 = 60
60 – 5 = 55
55 – 7 = 48
28 – 13 = 15
48 – 9 = 39
15 – 15 = 0
39 – 11 = 28
Square Root by Prime Factorization Method
Prime factorization of any number means to represent that number as a product of prime numbers. To find the square root of a given number through the prime factorization method, we follow the steps given below:
- Step 1: Divide the given number into its prime factors.
- Step 2: Form pairs of factors such that both factors in each pair are equal.
- Step 3: Take one factor from the pair.
- Step 4: Find the product of the factors obtained by taking one factor from each pair.
- Step 5: That product is the square root of the given number.
Let us find the square root of 144 by this method.
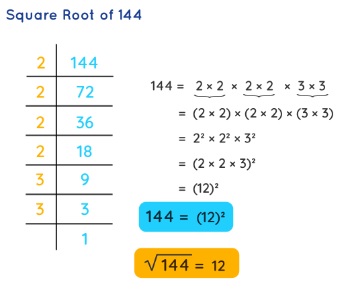
Example : Calculate the square root of 784 using prime factorization method.
Solution: List the prime factors of 784.
784 = 2 × 2 × 2 × 2 × 7 × 7
√784 = 2 × 2 × 7 = 28
Finding Square Root by Estimation Method
Estimation and approximation refer to a reasonable guess of the actual value to make calculations easier and more realistic. This method helps in estimating and approximating the square root of a given number. Let us use this method to find √15. Find the nearest perfect square number to 15. 9 and 16 are the perfect square numbers nearest to 15. We know that √16 = 4 and √9 = 3. This implies that √15 lies between 3 and 4. Now, we need to see if √15 is closer to 3 or 4. Let us consider 3.5 and 4. Since 3.52 = 12.25 and 42= 16. Thus, √15 lies between 3.5 and 4 and is closer to 4.
Let us find the squares of 3.8 and 3.9. Since 3.82 = 14.44 and 3.92 = 15.21. This implies that √15 lies between 3.8 and 3.9. We can repeat the process and check between 3.85 and 3.9. We can observe that √15 = 3.872.
This is a very long process and time-consuming.
Example: Estimate the square root of 300.
Solution: We know that, 300 comes between 100 and 400 i.e. 100 < 300 < 400.
Now, √100 = 10 and √400 = 20.
So, we can say that
10 < √300 < 20.
We can further estimate the numbers as we know that 172 = 289 and 182 = 324.
Thus, we can say that the square root of √300 = 17 as 289 is much closer to 300 than 324.
Calculating Square Root by Long Division Method
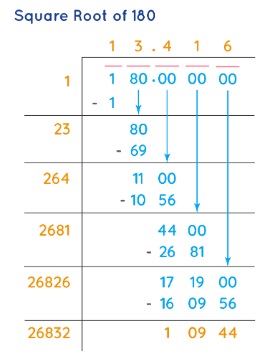
Long division is a method for dividing large numbers into steps or parts, breaking the division problem into a sequence of easier steps. We can find the exact square root of any given number using this method. Let us understand the process of finding square root by the long division method with an example. Let us find the square root of 180.
- Step 1: Place a bar over every pair of digits of the number starting from the units' place (right-most side). We will have two pairs, i.e., 1 and 80
- Step 2: We divide the left-most number by the largest number whose square is less than or equal to the number in the left-most pair.
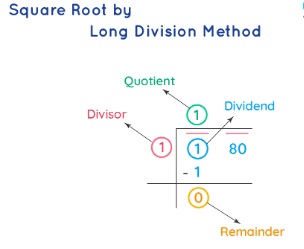
Step 3: Bring down the number under the next bar to the right of the remainder. Add the last digit of the quotient to the divisor. To the right of the obtained sum, find a suitable number which, together with the result of the sum, forms a new divisor for the new dividend that is carried down.
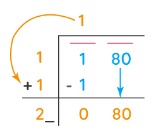
Step 4: The new number in the quotient will have the same number as selected in the divisor. The condition is the same — as being either less than or equal to the dividend.
Step 5: Now, we will continue this process further using a decimal point and adding zeros in pairs to the remainder.
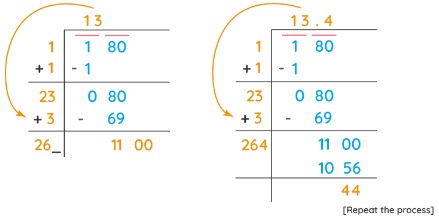
Step 6: The quotient thus obtained will be the square root of the number. Here, the square root of 180 is approximately equal to 13.4 and more digits after the decimal point can be obtained by repeating the same process as follows.
Example: Calculate the square root of √729 using division method.
Solution:

Thus, √729 = 27.
Square Roots of Decimals
To find the square root of a decimal number we have to put bars on the primary part of the number in the same manner as we did above. And for the digits on the right of the decimal we have to put bars starting from the first decimal place.
Rest of the method is same as above. We just need to put the decimal in between when the decimal will come in the division.
Example
Find √7.29 using division method.
Solution:

Thus, √7.29 = 2.7
Remark: To put the bar on a number like 174.241, we will put a bar on 74 and a bar on 1 as it is a single digit left. And in the numbers after decimal, we will put a bar on 24 and put zero after 1 to make it double-digit.
174. 24 10
Square Root Table
The square root table consists of numbers and their square roots. It is useful to find the squares of numbers as well. Here is the list of square roots of perfect square numbers and some non-perfect square numbers from 1 to 10.
| Number | Square Root |
|---|---|
| 1 | 1 |
| 2 | 1.414 |
| 3 | 1.732 |
| 4 | 2 |
| 5 | 2.236 |
| 6 | 2.449 |
| 7 | 2.646 |
| 8 | 2.828 |
| 9 | 3 |
| 10 | 3.162 |
The numbers that are not perfect squares are irrational numbers.
Square Root Formula
The square root of a number has the exponent of 1/2. The square root formula is used to find the square root of a number. We know the exponent formula: n√x = x1/n. When n = 2, we call it square root. We can use any of the above methods for finding the square root, such as prime factorization, and so on. 91/2 = √9 = √(3×3) = 3. So, the formula for writing the square root of a number is √x= x1/2.
Square Number : Any natural number ‘p’ which can be represented as y2, where y is a natural number, then ‘p’ is called a Square Number.
Example
4 = 22
9 = 32
16 = 42
Where 2, 3, 4 are the natural numbers and 4, 9, 16 are the respective square numbers.
Such types of numbers are also known as Perfect Squares.
Some of the Square Numbers

Properties of Square Numbers
- We can see that the square numbers are ending with 0, 1, 4, 5, 6 or 9 only. None of the square number is ending with 2, 3, 7 or 8.
- Any number having 1 or 9 in its one’s place will always have a square ending with 1.
| Number | Square Number |
| 1 | 1 |
| 9 | 81 |
| 11 | 121 |
| 19 | 361 |
| 21 | 441 |
- Any number which has 4 or 6 in its unit’s place, its square will always end with 6.
| Number | Square Number |
| 4 | 16 |
| 16 | 256 |
| 24 | 576 |
| 36 | 1296 |
| 44 | 1936 |
- Any number which has 0 in its unit’s place, its square will always have an even number of zeros at the end.
| Number | Square number |
| 10 | 100 |
| 50 | 2500 |
| 100 | 10000 |
| 150 | 22500 |
| 400 | 160000 |
Some More Interesting Patterns
1. Adding Triangular Numbers
If we could arrange the dotted pattern of the numbers in a triangular form then these numbers are called Triangular Numbers. If we add two consecutive triangular numbers then we can get the square number.

2. Numbers between Square Numbers
If we take two consecutive numbers n and n + 1, then there will be (2n) non-perfect square numbers between their squares numbers.
Example
Let’s take n = 5 and 52 = 25
n + 1 = 5 + 1 = 6 and 62 = 36
2n = 2(5) = 10
There must be 10 numbers between 25 and 36.
The numbers are 26, 27, 28, 29, 30, 31, 32, 33, 34, 35.
3. Adding Odd Numbers
Sum of first n natural odd numbers is n2.

Any square number must be the sum of consecutive odd numbers starting from 1.
And if any natural number which is not a sum of successive odd natural numbers starting with 1, then it will not be a perfect square.
4. A Sum of Consecutive Natural Numbers
Every square number is the summation of two consecutive positive natural numbers.
If we are finding the square of n the to find the two consecutive natural numbers we can use the formula

Example
52 = 25

12 + 13 = 25
Likewise, you can check for other numbers like
112 = 121 = 60 + 61
5. The Product of Two Consecutive Even or Odd Natural Numbers
If we have two consecutive odd or even numbers (a + 1) and (a -1) then their product will be (a2- 1)
Example
Let take two consecutive odd numbers 21 and 23.
21 × 23 = (20 - 1) × (20 + 1) = 202 - 1
6. Some More Interesting Patterns about Square Numbers

Finding the Square of a Number
To find the square of any number we needed to divide the number into two parts then we can solve it easily.
If number is ‘x’ then x = (p + q) and x2 = (p + q)2
You can also use the formula (p + q)2 = p2 + 2pq + q2
Example
Find the square of 53.
Solution:
Divide the number in two parts.
53 = 50 + 3
532 = (50 + 3)2
= (50 + 3) (50 + 3)
= 50(50 + 3) +3(50 + 3)
= 2500 + 150 + 150 + 9
= 2809
1. Other pattern for the number ending with 5
For numbers ending with 5 we can use the pattern
(a5)2 = a × (a + 1)100 + 25
Example
252 = 625 = (2 × 3) 100 + 25
452 = 2025 = (4 × 5) 100 + 25
952 = 9025 = (9 × 10) 100 + 25
1252 = 15625 = (12 × 13) 100 + 25
2. Pythagorean Triplets
If the sum of two square numbers is also a square number, then these three numbers form a Pythagorean triplet.
For any natural number p >1, we have (2p) 2 + (p2 -1)2 = (p2 + 1)2. So, 2p, p2-1 and p2+1 forms a Pythagorean triplet.
Example
Write a Pythagorean triplet having 22 as one its member.
Solution:
Let 2p = 6
P = 3
p2 + 1 = 10
p2 - 1 = 8.
Thus, the Pythagorean triplet is 6, 8 and 10.
62 + 82 = 102
36 + 64 = 100

