Key Concept
Statistics: Statistics is the study of collection, organization, analysis and interpretation of data.
Data :A distinct piece of information in the form of fact or figures collected or represented for any specific purpose is called Data. In Latin, it is known as the Datum.
Collection of Data :Data are generally of two types
- Primary Data
- Secondary Data
Primary Data
Data collected from any firsthand experience for an explicit use or purpose is known as Primary Data
Secondary data
Data collected by any third party for a different purpose other than the user is known as Secondary Data.
Presentation of Data
After collecting data it is important to present it in a meaningful manner. There are many ways to present data.
1. Ungrouped Data
a. Raw Data- If there is no change in the data and it is in the same form as it is collected then it is said to be raw data.
Example
The marks obtained by 10 students in a Sanskrit test are
55 36 95 73 60 42 25 78 75 62
Range- The difference between the highest and the lowest number of data is called Range.
b. Frequency Distribution- When the number of items is large then we can convert it into the tabular form which is called a Frequency Distribution Table.
Frequency is the number of times the item comes in the table.
2. Grouped Data
To present the very large number of items in a data we use grouped distribution table.

a. Class Interval – The group used to classify the data is called the class interval i.e. 20 – 30, 30 – 40.
b. Upper Limit - In each class interval, the greatest number is the upper-class limit.
c. Lower Limit – In each class interval, the smallest number is the lower class limit.
d. Class Size - It is the difference between the upper limit and the lower limit i.e. 10.
e. Class Mark – The midpoint of each class interval is the class mark.

Grouped data could be of two types as below:-
Inclusive or discontinuous Frequency Distribution – If the upper limit of one class is different from the lower limit next class then it is said to be an Inclusive or discontinuous Frequency Distribution.
Exclusive or continuous Frequency Distribution – If the upper limit of one class is the same as the lower limit of the next class then it is said to be exclusive or continuous Frequency Distribution
Graphical Representation of Data
As you know a picture is better than thousand words so represent data in an easier way is to represent it graphically. Some of the methods of representing the data graphically are
1. Bar Graph
It is the easiest way to represent the data in the form of rectangular bars so it is called Bar graph.
- The thickness of each bar should be the same.
- The space between in bar should also be same.
- The height of the bar should be according to the numerical data to be represented.
Example
Represent the average monthly rainfall of Nepal for the first six months in the year 2014.
| Month | Jan | Feb | Mar | Apr | May | Jun |
| Average rainfall | 45 | 65 | 40 | 60 | 75 | 30 |
Solution
- On the x-axis mark the name of the months.
- On the y-axis mark the class interval which we have chosen.
- Then mark the average rainfall respective to the name of the month by the vertical bars.
- The bars could be of any width but should be same.
- This is the required bar graph.

2. Histogram
It is like the Bar graph only but it is used in case of a continuous class interval.
- The class intervals are to be taken along an x-axis.
- The height represents the frequencies of the respective class intervals.
Example
Draw the histogram of the following frequency distribution.
| Daily earnings (in Rs) | 700 – 750 | 750 – 800 | 800 – 850 | 850 – 900 | 900 – 950 | 950 – 1000 |
| No. of stores | 6 | 9 | 2 | 7 | 11 | 5 |
Solution
- Mark the daily earnings on the x-axis.
- Mark the no. of stores on the y-axis.
- As the scale is starting from 700 so we will mark the zigzag to show the break.
- Mark the daily earnings through the vertical bars.

3. Frequency Polygon
To draw the frequency polygon
- First, we need to draw a histogram
- Then join the midpoint of the top of the bars a line segment and the figure so obtained is required frequency polygon.
- The midpoint of the first bar is to be joined with the midpoint of the imaginary interval of the x-axis
- The midpoint of the last bar is to be joined with the midpoint of the next interval of the x-axis.

If we need to draw the frequency polygon without drawing the histogram then first we need to calculate the class mark of each interval and these points will make the frequency polygon.
Example
Draw the frequency polygon of a city in which the following weekly observations were made in a study on the cost of living index without histogram.

Step 1: First of all we need to calculate the class mark of each class interval.
Step 2: Take the suitable scale and represent the class marks on the x-axis.
Step 3: Take the suitable scale and represent the frequency distribution on the y-axis.
Step 4: To complete the frequency polygon we will join it with the x-axis before the first class and after the last interval.
Step 5: Now plot the respective points and join to make the frequency polygon.

Measures of Central Tendency
To make all the study of data useful, we need to use measures of central tendencies. Some of the tendencies are
1. Mean
The mean is the average of the number of observations. It is calculated by dividing the sum of the values of the observations by the total number of observations.
It is represented by x bar or .
.
The mean of n values x1, x2, x3, ...... xn is given by
of n values x1, x2, x3, ...... xn is given by

Mean of Grouped Data (Without Class Interval)
If the data is organized in such a way that the frequency is given but there is no class interval then we can calculate the mean by


where, x1, x2, x3,...... xn are the observations
f1, f2, f3, ...... fn are the respective frequencies of the given observations.
Example

Here, x1, x2, x3, x4, and x5 are 20, 40, 60, 80,100 respectively.
and f1 , f2 , f3 , f4, f5 are 40, 60, 30, 50, 20 respectively.

2. Median
The median is the middle value of the given number of the observation which divides into exactly two parts.
For median of ungrouped data, we arrange it in ascending order and then calculated as follows

- If the number of the observations is odd then the median will be
 As in the above figure the no. of observations is 7 i.e. odd, so the median will be
As in the above figure the no. of observations is 7 i.e. odd, so the median will be term.
term.

= 4th term.
The fourth term is 44.
- If the number of observations is even then the median is the average of n/2 and (n/2) +1 term.
Example
Find the median of the following data.

1. First, we need to arrange it in ascending order.
4, 6, 7,8,10,12,12,13
2. The no. of observation is 8. As the no. of observation is even the median is the average of n/2 and (n/2)+1.
3.
4. 4th term is 8 and the 5th term is 10.
5. So the median
3. Mode
The mode is the value of the observation which shows the number that occurs frequently in data i.e. the number of observations which has the maximum frequency is known as the Mode.
Example
Find the Mode of the following data:
15, 20, 22, 25, 30, 20,15, 20,12, 20
Solution
Here the number 20 appears the maximum number of times so
Mode = 20.
Remark: The empirical relation between the three measures of central tendency is
3 Median = Mode + 2 Mean
Question : The owner of a plant nursery wanted to test the effectiveness of a new type of fertilizer. He measured the heights of 5 plants, and then gave each an equal amount of fertilizer. Two weeks later, he measured the heights of the plants again. The graph shows the height of the plants before and after the addition of fertilizer.
What was the mean growth of the plants?

- 4.5cm
- 5cm
- 5.5cm
- 6cm
| Age group (in years) | 10-16 | 17-23 | 24-30 | 31-37 | 38-44 | 45-51 | 52-58 |
| No. of illiterate persons | 175 | 325 | 100 | 150 | 250 | 400 | 525 |
Draw a histogram to represent the above data.
| Age group (in years) | 10-16 | 17-23 | 24-30 | 31-37 | 38-44 | 45-51 | 52-58 |
| No. of illiterate persons | 175 | 325 | 100 | 150 | 250 | 400 | 525 |
The histogram is the graphical representation of a frequency distribution in the form of rectangles, such that there is no gap between any two successive rectangles.
Clearly, the given frequency distribution is in inclusive form, that is there is a gap between the upper limit of a class and the lower limit of the next class.
Therefore, we need to convert the frequency distribution in exclusive form, as shown below:
| Age group ( in years) | 9.5-16.5 | 16.5-23.5 | 23.5-30.5 | 30.5-37.5 | 37.5-44.4 | 44.5-51.5 | 51.5-58.5 |
| No. of illiterate persons | 175 | 325 | 100 | 150 | 250 | 400 | 525 |
To draw the required histogram, take class intervals, that is the age group, along x-axis and frequencies, that is the number of illiterate persons along the y-axis and draw rectangles. So, we get the required histogram.
Since the scale on x-axis starts at 9.5, a kink (break) is indicated near the origin to show that the graph is drawn to scale beginning at 9.5.

| Marks | 0−10 | 10−20 | 20−30 | 30−40 | 40−50 |
| Number of Students | 8 | 18 | 35 | 25 | 14 |
(ii) Show that the area under frequency polygon is equal to the area under histogram.
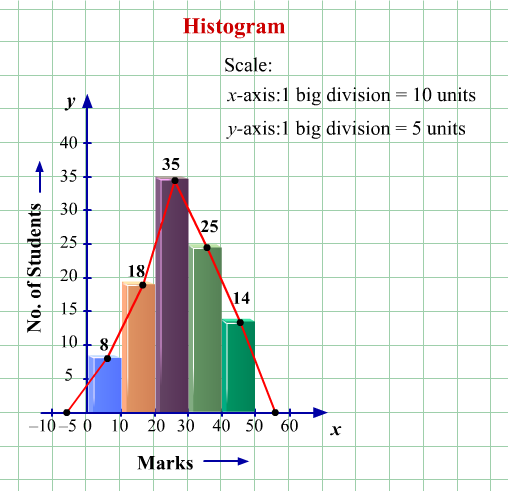
The area under a histogram and under a frequency polygon is the same because of the fact that we extend the first class interval to the left by half the size of class interval as the starting point of the frequency polygon. Similarly, the last class interval is extended to the right by the same amount as the end point of the frequency polygon. This ensures that the area that was excluded while joining the mid-points is included in the frequency polygon such that the area under the frequency polygon and the area of histogram is the same.
| Class intervals | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| Frequency | 30 | 24 | 52 | 28 | 46 | 10 |
Sol:The given frequency distribution is as below:
| Class intervals | 20-25 | 25-30 | 30-35 | 35-40 | 40-45 | 45-50 |
| Frequency | 30 | 24 | 52 | 28 | 46 | 10 |
Take class intervals along x-axis and frequency along the y-axis and draw rectangles of width equal to the size of the class intervals and height equal to the corresponding frequencies. Thus we get required histogram.
Now take imaginary class intervals 15-20 at the beginning and 50-55 at the end, each with frequency zero and joins the midpoint of the top of the rectangle to get the required frequency polygon.


