Key Concept
- Plane Figures :The closed 2-D shapes are referred to as plane figures.
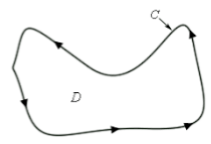
Here “C” is the boundary of the above figure and the area inside the boundary is the region of this figure. Point D comes in the area of the given figure.
- Perimeter: Sum of all sides of any closed 2-D shape.
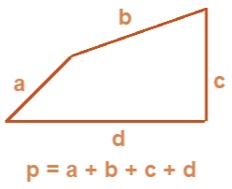
- Perimeter of a Triangle
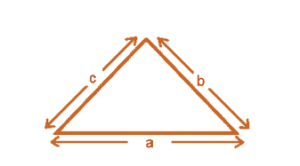
Perimeter of triangle = Sum of lengths of all sides = a + b + c.
If the given triangle is equilateral that is if all the sides are equal (a = b = c),
then its perimeter is equal to 3 × length of one side of the triangle.
- Perimeter of a Rectangle
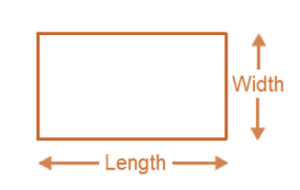
Perimeter of a rectangle = Sum of all sides
= length + breadth + length + breadth
Thus, Perimeter of a rectangle = 2 × (length + breadth)
- Perimeter of a Square
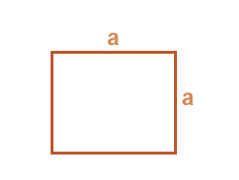
Perimeter of square = 4 × length of a side = 4a
- Perimeter of an ‘n’ Sided Polygon
A polygon is a closed shape made up of line segments.
Perimeter of n sided polygon = n× length of one side.
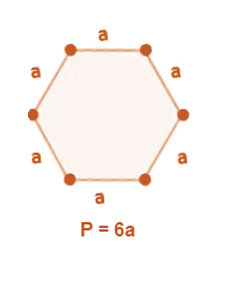
Example: Length of each side of a hexagon is a cm, then:
Perimeter of the hexagon = 6a cm
Area :Area refers to the surface enclosed by a closed figure.
To find the area of any irregular closed figure, we can put them on a graph paper with the square of 1 cm × 1 cm .then estimate the area of that figure by counting the area of the squares covered by the figure.
Here one square is taken as 1 sq.unit.
- Area of Square

Area of a square = Side × Side =Side2=a2, where a is the length of each side.
- Area of Rectangle

Area = length ( l ) × breadth ( b)
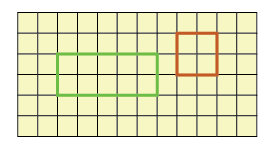
- In the given graph, if the area of each small square is 1 cm2, then
Area of rectangle = l×b = 5×2 = 10cm2
Area of square = a×a = 2×2 =4cm2 - Area of Triangle
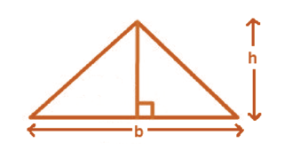
Area of triangle = (1/2) × base × height = (1/2) × b × h
Areas of different types of triangles
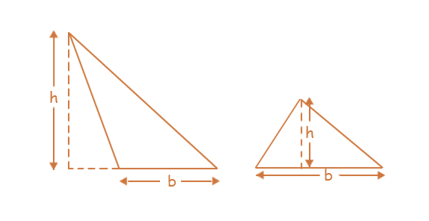
Consider an acute and an obtuse triangle.
Area of each triangle = (1/2) × base × height = (1/2) × b × h

