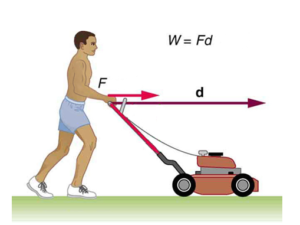
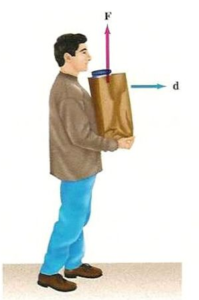
Concepts
‘Conditions of Work Done’: we can say that work is done if and only if:
- A force is applied to an object.
- If the object is displaced from one point to another point.
When you play a certain force ‘F Newton’ on an object and the object moves a distance of ‘ d meters’ in the direction where you applied the force then, the amount of work done can be calculated as:
|
Work done = Force * Displacement W = F * d |
Definition of Work Done: Work is defined as the product of the force applied on an object and displacement caused due to the applied force in the direction of the force. Work is a scalar quantity. It has no direction of its own but a magnitude.
|
SI unit of Work: N-m or J (Joule) |
What is 1 Joule Work?
A situation where 1 Newton force is applied on an object that can move the object by a distance of 1m in the direction of the applied force, then 1 joule of work is said to be done.
- Depending upon the direction of displacement and force applied the nature of work done may vary. Consider the table given below:
| The direction of Displacement | Work Done | Nature of Work Done | Angle between Force applied and Displacement occurred |
| Same as the direction of Force
|
W = F * d | Positive | 0o (Force and Displacement are Parallel to each other) |
| Opposite as direction of Force
|
W = -F * d | Negative | 180o |
| No change in position
|
W = F * 0 = 0 | Zero | 90o |
Energy
Any object that is capable of doing work processes some energy. The object can gain or lose energy depending upon the work done. If an object does some work it loses its energy and if some work is done on an object it gains energy.
Kinetic Energy
Every moving object possesses some energy called Kinetic Energy. As the speed of the object increases so is its kinetic energy.
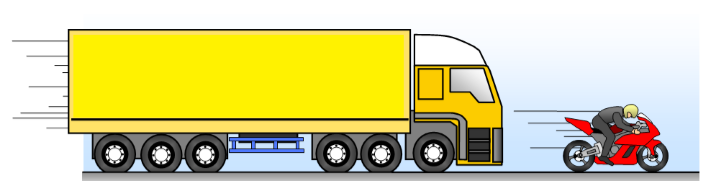
Formula for Kinetic Energy

Gravitational Potential Energy
The energy that the object gains at a height is called Gravitational Potential Energy. It is defined as the amount of work done required in raising an object above the ground up to a certain point against the gravity
Consider the example given below,
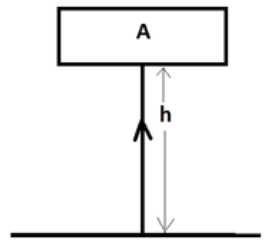
An object ‘A’ having mass ‘m’ is raised by height ‘h’ above the ground. Let us calculate the potential energy of object A at height ‘h’:
We know that,
|
W = F * d = F * h (height) And F = m * g (because the force is applied against gravity) So, W = m * g * h Hence potential energy of object A, Ep = m * g * h |
- Gravitational potential energy does not get affected due to the path taken by the object to reach a certain height.
Other forms of Energies:
- Mechanical Energy – It is the sum of kinetic and potential energy of an object. Therefore, it is the energy obtained by an object due to motion or by the virtue of its location. Example, a bicycle climbing a hill possesses kinetic energy as well as potential energy.
- Heat Energy – It is the energy obtained by an object due to its temperature. It is also called Thermal Energy. Example, energy possessed by a hot cup.
- Chemical Energy – It is the energy accumulated in the bonds of chemical compounds. Chemical energy is released at the time of chemical reactions. Example, energy possessed by natural gas and biomass.
- Electrical Energy – It is kind of kinetic energy caused due to the motion of electrons. It depends upon the speed of electrons. As the speed increases so does the electrical energy. Example, electricity produced by a battery, lightning at thunderstorms
- Light Energy – It is the energy due to light or electromagnetic waves. It is also called as Radiant Energy or Electromagnetic Energy. Example, energy from the sun
- Nuclear Energy – It is the energy present in the nucleus of an atom. Nuclear energy releases when the nucleus combines or separate. Therefore, we can say that every atom in this universe comprises of nucleus energy. Example, uranium is a radioactive metal capable of producing nuclear energy in nuclear power plants
- Sonic Energy – It is the energy produced by a substance as it vibrates. This energy flows through the substance in the form of sound waves. Example, music instruments produce sound energy
- Ionization Energy – It is the energy that binds electrons with its nucleus. It is thus the amount of energy required to remove one electron completely from its atom (called First Ionization Energy). Subsequently, the ionization energy increases as we remove the second electron from the atom ( called Second Ionization Energy).
- One form of energy can be transformed into other forms of energy.
Law of Conservation of Energy
According to the law of conservation of energy, the total amount of energy before and after transformation remains the same.
Consider the following example where an object of mass ‘m’ is made to fall freely from a height ‘h’.
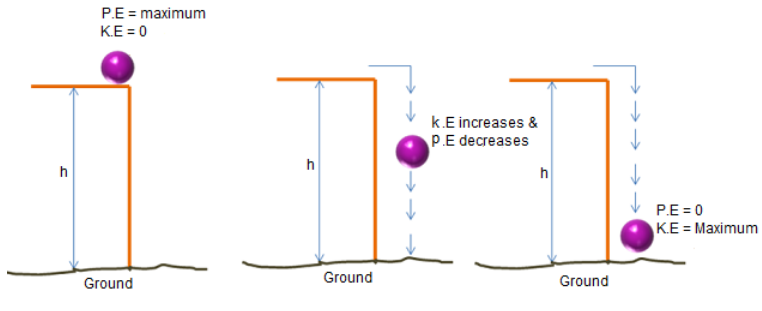
| Instant | Height at an instant | Kinetic Energy | Potential Energy | Sum of KE + PE = ME |
| 1 | Height = h | 0 (velocity is 0) | mgh | 0 + mgh |
| 2 | Height = k | (1/2) mv12 (velocity = v1) | mgk | (1/2) mv12 + mgk |
| 3 | Height = 0 | (1/2) mv22 (velocity = v2) | 0 | (1/2) mv22 + 0 |
We can see that the sum of kinetic energy and potential energy at every instant is constant. Hence, we can say the energy is conserved during transformation.
Power – The rate of doing work is defined as Power.
|
Power = Work Done / Time P = W/ t SI Unit: W (Watt) or J/s 1 kilowatt = 1000 watts 1 kW = 1000 W 1 W = 1000 J s-1 Average Power = Total Energy Consumed / Total Time taken |
Commercial Unit of Power
We cannot use Joule to measure power commercially. Instead, we use kilowatt-hour (kWh).
Commercial unit of energy = 1 kilowatt hour (kwh)
∴ 1 kWh = 1 kilowatt × 1 hour
= 1000 watt × 3600 seconds
= 3600000 Joule (watt × second)
1 kWh = 3.6 × 106 J.
∴ 1 kWh = 1 unit
The energy used in one hour at the rate of 1 kW is called 1 kWh.
Questions & Answers
Question 3. Answer the following questions.
- Enumerate the forms of energy?
- What is kinetic energy?
- Give the formula to calculate kinetic energy.
- What is the work energy theorem?
- Calculate the kinetic energy of a bullet of mass 8 g which is fired with a velocity of 80 m/s.
- Let us suppose that the weight of a body has mass 5 kg, it has a velocity of 10 m/s and is moving in a straight line with the acceleration of 20 m/s2. Calculate the kinetic energy after 10 seconds.
- If the mass of the van is 2000 kg, then calculate the work done to increase its velocity from 10 m/s to 20 m/s.
Answer 3:
- The forms of energy are:
- Mechanical energy
- Heat energy
- Chemical energy
- Electrical energy
- Light energy
- Kinetic energy is defined as the energy which is possessed by an object due to its motion.
- Work = Fs
According to the equation of motion,
V2 – u2 = 2as
S = v2 – u2/2a
Here, a is the uniform acceleration
u is the initial velocity
v is the final velocity.
F = ma
So on substitution of the values, we get,
W = ma.v2 -u2/2a = ½ m(v2 – u2)
If initial velocity = 0 then
W = ½ mv2
Since work done is equal to the kinetic energy, so
KE = ½ mv2
- According to the work energy theorem,
Total work is equal to the change in kinetic energy.
- Mass of the bullet = 8g
To convert it to kg, we get
8g = 8/1000 kg
Velocity = v = 80 m/s
To calculate the KE and applying the formula, we get
KE of bullet = ½ mv2 = ½ × 8/1000 × 80 × 80
= ½ × 8/1000 × 1600 = 25.6 J
- Mass of the body = m = 5 kg
Initial velocity = u = 10 m/s
Acceleration = a = 20 m/s2
Velocity = v = ?
KE = ?
We will use two formulas here,
First, we will calculate the v using the formula of equation of motion,
V = u + at
V = (u + at) m/s
We know the formula for kinetic energy,
KE = ½ m × (u + at)2
From both the above equation we will get,
KE = ½ × 5 × (10 + 20 × 10 )2
KE = ½ × 5 × 210 × 210 = 110250 J
- As per given in the question,
Mass = m = 2000 Kg
v1 = 10 m/s
v2 = 20 m/s2
To calculate the initial KE of the van,
KE1 = ½ mv2
KE = ½ × 2000 kg × (10 m/s)2
KE = 100000 J = 100 kJ
In order to calculate the final kinetic energy of the van, we will use the equation as,
KE2 = ½ mv2
KE2 = ½ × 2000 × (20 m/s)2 = 400000 J = 400 Kj
The work done will be calculated as,
Work done = change in KE = 400 kJ – 100kJ = 300kJ
So, it could be said that the KE of the van increases by 300 kJ when it speeds up from 10 m/s to 20 m/s.
Question 4. Answer the following questions in short.
- What is the SI unit of kinetic energy?
- Give examples of kinetic energy.
- What is potential energy?
- What is the SI unit of potential energy?
- Give examples of potential energy.
- What is the formula for potential energy?
- State the law of conservation of energy.
- Mention some important results which can be derived from the formula of the kinetic energy.
Answer 4:
- The SI unit of kinetic energy is Joules.
- Some of the examples of kinetic energy are: a target pierced by a bullet fired from a gun, a hammer which drives a nail into the wood, a running horse and a flowing river. All these have kinetic energy.
- The energy which is acquired or possessed by the body due to the change in position or shape is known as potential energy.
- The SI unit of potential energy is Joules.
- Some of examples of potential energy are like water stored in a dam and a stone lying on the roof of a building has potential energy due to its height. A wound spring of a watch has potential energy due to the change of its shape.
- Potential energy or PE = mgh. The work done is equal to the gain in energy of the body.
- According to the law of conservation of energy,
The energy can neither be created nor destroyed. It can only be transformed from one form to the other. It is very important to consider that the total energy before and after transformation remains constant always.
- Some of the important results which could be derived from the formula of kinetic energy are:
- Kinetic energy of KE is doubled when the mass of an object is doubled.
- The KE gets halved when the mass of the object is halved.
- KE becomes the four times when the speed of an object is doubled.
- KE becomes one-fourth when the speed of the object is halved.
- The heavy objects move at high speed so they have more KE.
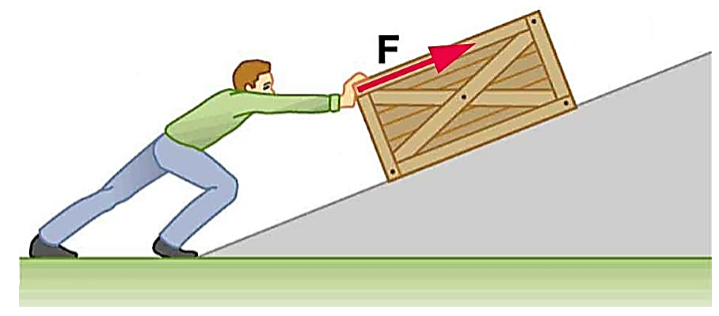
Question 5. An object is given as shown in the figure. The force of 7 N acts on the object, the displacement is 8 m . and it is in direction of the force. Let us suppose that the force is acting on the object through the displacement. In this case and the condition depicted in the figure, calculate the work done.
Answer 5:
As shown in the figure above,
Work done = W = Fs
Here the work done is positive because the force and the displacement are in the same direction.
W = 7 × 8 = 56 J
Question 6. When do we say that the work is done?
Answer 6: The work is said to be done when the force acting on the body causes some displacement. So the work is done by the force on the body.
Question 7. Present the equation of work done when the force is acting on the object in the direction of the displacement.
Answer 7: Work done will be positive because the force and displacement are in the same direction.
W = + Fs
Here F is the force and s is the displacement.
Question 8. What is 1 Joule of work?
Answer 8: This is the amount of work done on the object when a force of 1 Newton displaces it by 1 metre along the line of action of the force. This is called 1 Joule of work.
Question 9. A force of 140 N is exerted by a pair of bullocks on a plough. The field is ploughed 15 m long. Calculate how much work is done in ploughing the length of the field.
Answer 9: As given in the question,
Force = F = 140 N
Displacement = s = 15 m
Work done = W = + Fs
F and s are in the same direction.
W = Fs = 140 × 15 = 2100 J.
Question 10. Suppose that the kinetic energy of an object of mass m moving with a speed of 5 m/s is 25 J. When the velocity is increased three times what will be the kinetic energy?
Answer 10:
Mass of the body = m
Initial velocity = vi
KEi = ½ mvi2
The values given in the question are,
KEi = 25 J, vi = 5 m/s
25 J = ½ × m × 5 × 5
m = 25 × 2/ 5 × 5
m = 2 Kg
final velocity is becoming three times of initial velocity
vf = 3vi = 3 × 5 = 15 m/s
KE = ½ × m ×vf2 = ½ × 2 × 15 × 15 = 225 J
Question 11. Explain power. What is 1 watt of power? Calculate the power if the lamp consumes 1000 J of electrical energy in 10 s.
Answer 11: The power is defined as the rate of doing work or the rate at which the energy is transferred or used or transformed to other forms.
Suppose the work done is W in time t, then
Power = work/time = W/t
The unit of power is Watt or W. This is in honour of James Watt.
Kilowatt is used to express a larger rate of energy transfer.
1 Watt = 1 J/s
1kW = 1000 W = 1000 J/s
1 MW = 106 W
1 horsepower or HP = 746 W
To solve the problem in the given question,
Energy = 1000 J
Work done = W = 1000 J
Time = t = 10 s
Power of lamp = W/t = 1000/10 = 100-watt
Question 12. What is the average power?
Answer 12: The ratio of total work done to the total time taken is known as the average power.
Average power = total energy consumed/total time taken
Question 13. Justify the given question with the reason. What is the work done by the force of gravity on a satellite moving around the earth?
Answer 13: Work done in this case will be zero. This is because the angle between the force and the displacement in case of circular motion so the work done is zero.
Question 14. Multiple choice questions:
- Various factors are given below, find out the one on which the work done on an object does not depend.
- Displacement
- Force applied
- The angle between force and displacement
- Initial velocity of the object
Answer: (d) Initial velocity of the object
Explanation:
Work =W = F. d cosϴ
In the above equation, W is the work done
F is the force which is applied on the object. The displacement is d and ϴ is the angle between the force and the displacement. So it is clear that the work done on an object does not depend upon the initial velocity of the object.
- What about the total energy of the body when it falls freely towards the earth?
- increases
- decreases
- Remain constant
- It first increases but then it decreases.
Answer: c) Remains constant
Explanation:
As we know, the total energy of the system is always conserved. So when the object falls freely towards the earth, the energy remains constant. This means that the sum of the potential energy and the kinetic energy of the body would be the same at all the points.
- Which type of energy is possessed by the water stored in a dam?
- No energy
- Electrical energy
- Kinetic energy
- Potential energy
Answer: (d) Potential energy.
Explanation:
Water stored in the dam has potential energy because potential energy is stored energy, or, in other words,it could be said that it is the energy of position.
- In the case of negative work, what is the angle between the force and the displacement?
- 0
- 45 degrees
- 90 degrees
- 180-degree
Answer 4: (d) 180 degree
- A girl is carrying a school bag which has a mass of 3 kg on her back. The girl moves 200 m on a levelled road. If g = 10 m/s2 then what is the work done against the gravitational force?
- 6 × 103 J
- 6 J
- 0.6 J
- Zero
Answer 5: (d) Zero
- An electric bulb of 60 W burns for 5 hours a day. The electricity cost in 30 days of the month is at Rs 3 per unit is
- 270
- 27
- 2.70
- 2700
Answer 6: (b) 27
Cost of electricity = P × t × cost per kW
= 0.06 kW × (5 × 30) × 3 = 27
- A tank has water which has the mass m to a height h. Then the potential energy associated is
- mgh
- mg h/h
- this depends on how much radius the tank has
- zero
Answer: (b) mg h/2
This is the potential energy calculated based on the height will be up to the centre of gravity of tank.
- What is the total energy at any point on the path when the mass m falls from a height h.
- ½ mgh
- mgh/4
- mgh
- It depends on the height
Answer: C – mgh
This is according to the law of conservation.
Question 15. An example of some of the activities is given below. Just find out whether the work has been done or not.
- Aryan is swimming in a pond.
- A donkey is carrying the load on the back.
- A windmill is lifting water from the well.
- A green plant is carrying out photosynthesis.
- An engine is pulling a train
- Food grains are getting dried in the sun
- A sailboat is moving due to wind energy.
Answer 15:
- In this example, work is done because Aryan gets displaced due to the reaction force of water while swimming in the pond.
- The donkey is moving in the horizontal direction, and the force is being applied to the load in the vertical direction, so in this case the work done is zero.
- In this example, the windmill is doing the work of lifting water, and the moving blades of the windmill displace the water from the well in the direction of upwards.
- In this case, no work is being done because there is no displacement and no force is acting .
- The engine is exerting force, and the train is being displaced, so the work is being completed in this case.
- As seen, force and displacement are zero, so no work is done.
- The sailboat is moving due to the applied wind force, so the work is completed in this case.
Question 16. Describe the energy changes involved when the battery lights the bulb.
Answer 16: In this case, chemical energy is converted to electrical energy. So the final result is the combination of heat energy and light energy.
Question 17. Calculate the work done by the force when the force is acting on a mass of 20 kg and there is a change in velocity from 5 m/s to 2 m/s.
Answer 17: In the question, the following values are given,
Mass = m = 20 kg
u = 5 m/s
v = 2 m/s
Work = Change in Kinetic energy = ½ m (v2 – u2) = ½ × 20 × (22 – 52) = -210 J
This shows that the work is done in the opposite direction to the displacement of mass.
Question 18. Is there any violation of the law of conservation of energy when the potential energy of a freely falling object decreases progressively?
Answer 18: No, in this case, the law of conservation of energy is not violated because a freely falling body gains kinetic energy in an amount that is equal to the loss of potential energy. So overall, the total energy of the object remains conserved.
Question 19. When riding a bicycle, what type of energy transformation occurs?
Answer 19: While riding the bicycle, there is a conversion of the muscular energy of the rider to the kinetic energy of the bicycle.
Question 20. While pushing a heavy rock, you might fail to move it, so in this case, is there any transfer of energy that takes place? And the energy you spent, where did it go?
Answer 20: Yes, the energy that is used up is responsible for causing muscular contractions, and it is dissipated in the form of heat or sweating as well.
Question 21. In a house, 250 units of energy are consumed in a month. So how much energy is this in Joules?
Answer 21: As per the question,
Units consumed = 250 = 250 kWh
1 unit = 1 kWh = 3.6 × 106 J
250 kWh = 250 × 3.6 × 106 J = 9 × 108 J
Question 22. A 40 kg object is raised to a height of 5 m above the ground.What is its potential energy? If the object is allowed to fall, find its kinetic energy when it is half – way down.
Answer 22: m = 40 kg, h = 5 m, g = 9.8 m/s2
Potential energy = mgh = 40 × 5 × 9.8 m/s2 = 1960 J
When the height becomes half, potential energy gets halved = 1920/2 = 980 J
Loss in potential energy is equal to the gain in kinetic energy equal to 980 J.
Question 23. When there is no force acting on the object, can there be any displacement of the object? Clarify the answer.
Answer 23: If the object moves with constant velocity, then according to Newton’s first law of motion, the net force acting on it is zero. This states that an object will remain in a state of rest or of uniform motion in a straight line unless a net external unbalanced force acts on it. Here the force acting is zero, but the displacement is non – zero.
Question 24. A woman is holding a bundle of hay over her head for 30 minutes, and she gets tired. Has she done any work or not? Justify your answer.
Answer 24. The displacement of the person is zero, so this means that the person has not done any work.
Question 25. How much energy does an electric heater use in 10 hours when the heater is rated at 1500 watts?Answer 25: Power = P = 1500 W
On conversion P = 1.5 kW, t = 10 hour
Energy = Pt = 1.5 kW × 10 h = 15 kWh
Question 26. An object of mass m is moving with a constant velocity v. calculate the work done on the object in bringing it to rest.
Answer 26: Work = ½ × mass × (velocity)2
W = ½ mv2
Question 27. Calculate the work required to be done to stop a car of 1500 kg moving at a velocity of 60 km/h?
Answer 27: Mass = m = 1500 kg
Velocity = v = 60 km/h = 60 × 5/18 m/s
Work done = kinetic energy = ½ mv2
Work done = ½ × 1500 × ( 60 × 5/18 ) × (60 × 5/18) = 208333.3 J = 208.3 kJ
Question 28. What is the difference between a kilowatt and a kilowatt hour? Suppose a waterfall has a height of 20 m and 20,00 tonnes of water falls from it in a minute. If this energy is utilised then how much is the equivalent power? Calculate.
Answer 28: Kilowatt is the unit of power, while kilowatt hour is the unit of electrical energy consumed.
m = 2000 × 103 kg
h = 20 m
t = 1 min = 60 s
Power of falling water = mgh/t
= 2000 × 103 × 10 × 20/ 60
= 6.67 × 106 W or 6.67 MW
Question 29. How can power be related to the speed at which a body could be lifted? A man is working at a power of 100 W. How many kilograms will he be able to lift at a constant speed of 1 m/s2. The value of g is 10 m/s 2.
Answer 29:
We know the formula that,
Power = force × velocity
P = 100 Watt, v = 1 m/s2
F = P/v =100N
F = mg
So, m = F/g = 100N/10 ms2
= 10 kg
The answer is 10 kg can be lifted by the man.
Question 30. Compare the power for (a) and (b). These are moving upward against the force of gravity.
- A butterfly has a mass of 1 gram and is flying upward at a rate of 0.5 m/s.
- A 250 g of a squirrel climbing up a tree at a rate of 0.5 m/s
Answer 30:
- P = Fv = mgv
m = 1 g = 10-3 kg, v = 0.5 m/s
Power of the butterfly will be calculated as
P = 10-3 × 10 × 0.5 = 5 × 10-3 = 0.005 Watt
- Mass = m = 250 g = 250 × 10-3 kg
v = 0.5 m/s
Power of squirrel = 250 × 10-3 × 10 × 0.5
P = 1250 × 10-3 = 1.25 watt
The answer could be written as the power of squirrels is more than that of the butterfly.
Question 31. When the momentum of the object is zero, can the object have any mechanical energy?
Answer 31: Yes, it is possible. When a body is thrown up, potential energy in the form of mechanical energy is non-zero at the highest point of a projectile, even if kinetic energy is zero due to the zero velocity.
Question 32. Is it possible for the object to have momentum even if its mechanical energy is zero? Explain
Answer 32. No, because when energy is zero, both potential energy and kinetic energy are zero. So this makes both the momentum and the velocity zero.
Question 33. The motor pump has a power of 2kW. The pump can raise how much water per minute to a height of 10 m?
Answer 33: As per the question,
m is raised to the height h
PE gained = mgh
Power = work done / time = mgh/t
m/t = P/gh
= 2 × 103/10 × 10 = 20 kg/s
Mass of water pumped per minute
= 20 × 60 = 1200 kg.
Question 34. For the work to be done on an object list two conditions which need to be satisfied.
Answer 34: There are two conditions here, a force should act on the object and there should be a displacement in the object.
Question 35. A few situations are given below. Analyse them and comment on where work is said to be done. Mention the answer with an explanation.
- A man is pushing the rock, which is hard and huge, but it is not moving.
- A bullock is pulling a cart up to 1 km on the road.
- A girl is pulling a trolley for about 2 m distance.
- A person standing with a heavy bag on his head.
Answer 35:
- Since the displacement is zero, the work done is also zero.
- In this situation, the work done is positive.
- In this situation, the work done is positive.
- In this case, since the displacement is zero, the work done is also zero.
Question 36. Define what is 1kWh?
Answer 36: If a 1 kW device is operated for 1 hour, the energy consumed by the device is 1 kWh.
Question 37. Suppose an object is lifted by the crane in the time t to a height of h. What is the relation between the power of a crane to the speed at which it is lifting the object?
Answer 37: power = work done / time taken
Mass = m, height = h
Work done = mgh
P = mgh / t = mg (h/t)
Is the speed at which the body is lifted, v = h/t
Since it is distance / time
Force = F = mg
Power = (mg) (h/t)
Power = mg v = Fv
Question 38. An electric iron of 1600 W is used for 45 minutes per day. Find the amount of electric energy consumed in the month of March.
Answer 38: Power = P = 1600 W = 1.6 kW
t = 45 = 45/60 h
The time of consumption in March will be calculated as follows: March has 31 days
T = (45/60 × 31) h
Energy consumed = PT = 1.6 × 45/60 × 31 = 37.2 units
Question 39. How much work is done by the moon when the moon is experiencing a gravitational force because of the earth and it is revolving around the earth in a circular orbit.
Answer 39: In this case, the work done by the moon will be zero because, towards the centre of the orbit, centripetal force is acting and the direction of the displacement is tangential to the orbit.
Question 40. What are the conditions under which the work done is zero.
Answer 40. The work done by body is zero, if
- There is no displacement occurring despite the application of force.
- W = Fs cos ϴ and cos 90 degree = 0, so displacement in the body is perpendicular to the applied force.
Question 41. How much work is done by the person when a 2 m high person is holding a trunk on his head that has a weight of 25 kg and is standing at roadway bus terminals.
Answer 41: There are various conditions mentioned in the question, but there has been no displacement, so the work done in this case will be zero.
Question 42. State whether the given statement is true or false.
- A student is studying hard for the exam and is doing more work than the baby who is crawling from one corner of the room to the other corner of the room.
- Energy is converted from one form to the other but only in a few cases.
- Work done is a vector quantity.
- Energy is a scalar quantity while momentum is a vector quantity.
- A moving truck has more kinetic energy than a bicycle which is moving with the same speed.
- Horse power is used to measure the power of heavy machines.
Answer :
- False. Here the work done by the student is zero because there is no displacement. Baby is crawling and is displaced from one corner to the other.
- False.
- False
- True
- True
- True
Question 43. Fill in the blanks:
- Work done can be__________, _________ or___________.
- _________work is done by the satellite when it is revolving around the earth.
- 60 W power means the device uses 60 Joule of energy is _________hour.
- When non-zero force and displacement are observed with zero work done, the angle between the force and displacement is __________.
- Engine require fuel like for example petrol and diesel. The combustion of fuel provides ____________ to them.
- Living beings and machines as well need _________ to work.
- Living beings get energy from _________
- Machines get energy from __________ and _________
Answer:
- Work done can be positive, negative, or zero.
- Zero work is done by the satellite when it is revolving around the earth.
- 60 W power means the device uses 60 Joule of energy is 1/3600 hour.
- When non-zero force and displacement are observed with zero work done, the angle between the force and displacement is 90 degrees
- Engine require fuel like for example petrol and diesel. The combustion of fuel provides energy to them.
- Living beings and machines as well need energy to work.
- Living beings get energy from food
- Machines get energy from electricity and fuel
Question 44. Answer the following questions:
1.A raised hammer possesses which type of energy?
- What happens to the potential energy in each case when the slinky is compressed or stretched.
3.A moving car possesses which type of energy?
- What happens to the rubber band when it is stretched, mention about the work done.
- Which type of kinetic energy is possessed by the running athlete.
- energy is possessed by the different objects due to their motion. Give examples in this case.
- Which is the term used to sum of kinetic energy and potential energy.
- 1 calorie equals how many joules?
- I kilojoule equals how many joules?
- What is the CGS unit of energy and how it is related to the SI unit.
- Two persons A and B are asked to complete a work in 1 hour and 2 hours respectively. Who is more powerful and why?
Answer 44.
1.The raised hammer possesses potential energy.
- The potential energy of the slinky will increase in each case.
- The type of energy by a moving car is kinetic energy.
- Suppose a rubber band is stretched, work done on the rubber band is stored as its potential energy since it is not used to cause a change in speed or velocity of any object.
- The energy possessed by a running athlete is the kinetic energy.
- Few of the examples are falling coconut, speeding car, flying aircraft, flowing water, etc.
- The sum of the kinetic energy and the potential energy is the mechanical energy.
- 1 calorie is equal to the 4.186 Joule.
- 1 kilojoule is equal to the 103 Joule.
- The CGS unit of energy is erg. The value of 1 Joule equals 107 erg.
- Person A is more powerful because he does work in less time as compared to B.
Question 45. At what position the potential and kinetic energies are going to be maximum in an oscillating pendulum?
Answer 45: In this case of an oscillating pendulum, the potential energy will be maximum at the extreme position and the kinetic energy will be maximum at the mean position.
Question 46. The mass of a body is 1 kg, at what speed it will have the kinetic energy of 1 Joule?
Answer 46: Kinetic energy = 1 Joule
Mass = m = 1 kg
KE = ½ mv2
1 = ½ × 1v2
This implies that
V2 = 2
V = 2 m/s
Question 46. Mention the change in the kinetic energy when the speed of the body is halved?
Answer 46:
KE = ½ mv2
From the above equation it is clear that the KE is directly proportional to the v2
So as mentioned if v is v/2, then v2 will become v2/4
Question 47. A horse and a dog are running at the same speed. The horse has a mass of 210 kg and the dog has a mass of 25 kg. Which out of these two have more kinetic energy and how?
Answer 47: As we know, kinetic energy and mass are directly proportional to each other.
Mass of the horse is greater than the mass of the dog.
So it could be said that horses possess greater kinetic energy.
Question 48: The examples are given below. Mention the type of energy transformation.
- Arrow is released from the bow.
- Solar cell use.
- Electric motor
- Electric generator
- Steam engine
- Electric bulb
- Dry cell
Answer 48:
- Potential energy of the bow string will convert to the kinetic energy of the arrow.
- Light energy will get converted to electrical energy.
- Electrical energy will get converted to mechanical energy.
- Mechanical energy will get converted to electrical energy.
- Heat energy will get converted to kinetic energy.
- Electrical energy will get converted to light energy.
- Chemical energy will get converted to electrical energy.
Question 49. A force of 10 N acts on a body which has a mass of 2 kg for a period of 3 seconds. Find out the kinetic energy acquired by the body in 3 seconds.
Answer 49:
Kinetic energy = work done on the body
Mass = m = 2 kg
Time = t = 2 seconds
u = 0 and F = 10 N
acceleration = a = F/m = 10/2 = 5 m/s2
displacement = s = ut + ½ at2
= 0 + ½ × 5 × 3 × 3 = 22.5 m
Work done = Fs = 10 N × 22.5 m = 225 J
Question 50. What is the force which is applied by the brakes of the truck which has a mass of 1800 kg and is moving with a speed of 54 km/h. When the brakes are applied it stops with a uniform acceleration at a distance of 200 m. Calculate the force applied by the brakes of the truck and the work done before stopping.
Answer 50: mass = m = 1800 kg
u = 54 km/h = 54 × 5/18 = 15 m/s
v = 0
s = 200 m
retardation, a = v2 – u2/2s
a = -9/16 m/s2
F = ma = 1800 × -9/16
= -1012.5 N
Since the force is acting in the opposite direction to motion so the negative sign is used.
Work done = Fs = 1012.5 × 200 = 202500 J
Question 51. The mass of the scooter and the bike are in the ratio of 2 : 3, they are moving with the same speed at 108 km/h. What is the ratio of their kinetic energy?
Answer 51.
Kinetic energy is directly proportional to the mass of the body
Suppose mass of scooter = ms = 2m
Mass of the bike = mb = 3m
Kinetic energy of the scooter/ kinetic energy of the bike = ms/mb = 2m/3m = 2:3
Question 52. A heavy ball falls on the thick bed of wet sand from different heights-50 cm, 1 m, and 2 m, respectively. The depression created in the sand is measured. Identify which depression is the deepest and which one is the shallowest. Give a reason for the answer.
Answer 52:
When the ball is dropped from a height of 2 m, the impression made by the wall is the deepest, as it transfers the most energy when it hits the wet sand.On the other hand, when the ball is dropped from a height of 50 cm, the impression made by the ball is the shallowest because the energy transferred by the ball to the wet sand is the least.
Question 53. Suppose there is a trolley and a block of a mass m is placed in front of it. When the mass is kept on the trolley it moves, hits the block and then it gets displaced. From where does the block get the energy? If the mass on the pan increases, will there be more work done, and what type of energy is possessed by the trolley?
Answer 53: First of all, the block is getting the energy because work is done on it by moving the trolley. When more work is done on the block as the trolley moves faster, then there will be more work done. The energy possessed by the trolley is kinetic energy.
Question 54. Explain what you understand of energy conversion by the phenomena which are given below.
- How do green plants prepare food?
- How the air moves from one place to the other.
- How are fossil fuels formed?
Answer 54:
- The green plants prepare food by converting light energy from the sun into the chemical energy of food in the form of sugars.
- Thermal energy from the sun gets converted into the kinetic energy of air, so convection currents are set up in the air due to the uneven heating of the earth by the sun.
- Fossil fuels are formed when solar energy is stored as chemical energy in plants. These are buried in the earth over millions of years, and eventually they get converted into fossils.