Quadrilaterals – Hari Shanker Pandey Sewa Samiti

Concepts

Quadrilateral

Any closed polygon with four sides, four angles and four vertices are called Quadrilateral. It could be regular or irregular.

Angle Sum Property of a Quadrilateral

The sum of the four angles of a quadrilateral is 360°

If we draw a diagonal in the quadrilateral, it divides it into two triangles.

And we know the angle sum property of a triangle i.e. the sum of all the three angles of a triangle is 180°.

The sum of angles of ∆ADC = 180°.

The sum of angles of ∆ABC = 180°.

By adding both we get ∠A + ∠B + ∠C + ∠D = 360°

Hence, the sum of the four angles of a quadrilateral is 360°.

Example

Find ∠A and ∠D, if BC∥ AD and ∠B = 52° and ∠C = 60° in the quadrilateral ABCD.

Solution:

Given BC ∥ AD, so ∠A and ∠B are consecutive interior angles.

So ∠A + ∠B = 180° (Sum of consecutive interior angles is 180°).

∠B = 52°

∠A = 180°- 52° = 128°

∠A + ∠B + ∠C + ∠D = 360° (Sum of the four angles of a quadrilateral is 360°).

∠C = 60°

128° + 52° + 60° + ∠D = 360°

∠D = 120°

∴ ∠A = 128° and ∠D = 120 °.

Types of Quadrilaterals

S No.	Quadrilateral	Property	Image
1.	Trapezium	One pair of opposite sides is parallel.
2.	Parallelogram	Both pairs of opposite sides are parallel.
3.	Rectangle	a. Both the pair of opposite sides is parallel. b. Opposite sides are equal. c. All the four angles are 90°.
4.	Square	a. All four sides are equal. b. Opposite sides are parallel. c. All the four angles are 90°.
5.	Rhombus	a. All four sides are equal. b. Opposite sides are parallel. c. Opposite angles are equal. d. Diagonals intersect each other at the centre and at 90°.
6.	Kite	Two pairs of adjacent sides are equal.

Remark: A square, Rectangle and Rhombus are also a parallelogram.

Properties of a Parallelogram

Theorem 1: When we divide a parallelogram into two parts diagonally then it divides it into two congruent triangles.

∆ABD ≅ ∆CDB

Theorem 2: In a parallelogram, opposite sides will always be equal.

Theorem 3: A quadrilateral will be a parallelogram if each pair of its opposite sides will be equal.

Here, AD = BC and AB = DC

Then ABCD is a parallelogram.

Theorem 4: In a parallelogram, opposite angles are equal.

In ABCD, ∠A = ∠C and ∠B = ∠D

Theorem 5: In a quadrilateral, if each pair of opposite angles is equal, then it is said to be a parallelogram. This is the reverse of Theorem 4.

Theorem 6: The diagonals of a parallelogram bisect each other.

Here, AC and BD are the diagonals of the parallelogram ABCD.

So the bisect each other at the centre.

DE = EB and AE = EC

Theorem 7: When the diagonals of the given quadrilateral bisect each other, then it is a parallelogram.

This is the reverse of the theorem 6.

The Mid-point Theorem

1. If a line segment joins the midpoints of the two sides of the triangle then it will be parallel to the third side of the triangle.

If AB = BC and CD = DE then BD ∥ AE.

2. If a line starts from the midpoint of one line and that line is parallel to the third line then it will intersect the midpoint of the third line.

If D is the midpoint of AB and DE∥ BC then E is the midpoint of AC.

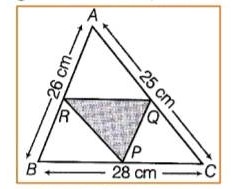
Important Question :There is a visit to a school by the Directorate of Education. Girls are asked to prepare Rangoli in a triangular shape. Dimension of ΔABC are 26cm ,28cm, and 25cm. Garland is to be placed along the side of ΔPQR, which is formed by joining mid-points of sides of ΔABC. (i) Find the length of the garland. (ii) Which values are depicted here?

Example

Prove that C is the midpoint of BF if ABFE is a trapezium and AB ∥ EF.D is the midpoint of AE and EF∥ DC.

Solution:

Let BE cut DC at a point G.

Now in ∆AEB, D is the midpoint of AE and DG ∥ AB.

By midpoint theorem, G is the midpoint of EB.

Again in ∆BEF, G is the midpoint of BE and GC∥ EF.

So, by midpoint theorem C is the midpoint of BF.

Hence proved.

Points to Remember

A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order.
A quadrilateral has four sides, four angles and four vertices.
Two sides of a quadrilateral having no common end point are called its opposite sides.
Two sides of a quadrilateral having a common end point are called its adjacent sides.
Two angles of a quadrilateral having common arm are called its adjacent angles.
Two angles of a quadrilateral not having a common arm are called its opposite angles.
A diagonal is a line segment obtained on joining the opposite vertices.
Sum of all the angles of a quadrilateral is 360 degree. This is known as the angle sum property of a quadrilateral.
If the non-parallel sides of trapezium are equal, it is known as isosceles trapezium.
Square, rectangle and rhombus are all parallelograms.
Kite and trapezium are not parallelograms.
A square is a rectangle.
A square is a rhombus.
A parallelogram is a trapezium.
Properties of parallelogram:
i. The opposite sides of a parallelogram are parallel.
ii. A diagonal of a parallelogram divides it in two congruent triangles.
iii. The opposite sides of a parallelogram are equal.
iv. The opposite angles of a parallelogram are equal.
v. The consecutive angles (conjoined angles) of a parallelogram are supplementary.
vi. The diagonals of a parallelogram bisect each other.
A quadrilateral is a parallelogram if:
i. each pair of opposite sides of a quadrilateral is equal, or
ii. each pair of opposite angles is equal, or
iii. if the diagonals of a quadrilateral bisect other, or
iv. if a pair of opposite sides is equal and parallel.
Mid-Point Theorem
The line segment joining the mid-point of any two sides of a triangle is parallel to the third sides and equal to half of it.
Converse of mid-point theorem
The line drawn through the mid-point of one side of a triangle parallel to the another side, bisects the third side.
If there are three or more parallel lines and the intercepts made by them on a transversal are equal, then the corresponding intercepts on any other transversal are also equal.