Concepts
Basic Concepts and Important Points
1. Two angles are called adjacent angles if
(a) they have the same vertex.
(b) they have a common arm and
(c) uncommon arms are on either side of the common arm.
2. Two adjacent angles are said to form a linear pair of angles, if their non-common arms are two opposite rays.
3. The sum of all the angles round a point is equal to 360°.
4. If two lines intersect, then the vertically opposite angles are equal.
5. A line which intersects two or more given lines at distinct points, is called a transversal of the lines.
6. Two angles on the same side of a transversal are known as corresponding angles if both lie either above the two lines or below the two lines.
7. The pairs of interior angles on the same side of the transversal are called consecutive interior angles.
8. If a transversal intersects two parallel lines, then each pair of corresponding angles are equal.
9. If a transversal intersects two parallel lines, then each pair of alternate interior angles are equal.
10. If a transversal intersects two parallel lines, then each pair of consecutive interior angles are supplementary.
11. A triangle whose sides are unequal, is called a scalene triangle.
12. A triangle, two of whose sides are equal in length, is called an isosceles triangle.
13. A triangle, all of whose sides are equal is called an equilateral triangle.
14. A triangle, each of whose angle is less than 90°, is called an acute triangle.
15. A triangle with one of its angle 90°, is called a right triangle.
16. A triangle with one of its angle greater than 90°, is known’s an obtuse triangle.
17. If a side of a triangle is produced, the exterior angle so formed is equal to the sum of two interior opposite angles.
18. If all sides of a polygon are equal, it is called a regular polygon.
19. Sum of all the interior angles of a polygon of n sides = (n – 2) × 180°, (n ≥ 3)
20. Each interior angle of a regular polygon on n sides 
21. Sum of all the exterior angles formed by producing the sides of polygon = 360°
22. Number of sides of polygon
23. Reflex angle: An angle whose measure is more than 180° but less than 360°, is called reflex angle.
24. The sum of angles forming a linear-pair is 180°.
25. Supplementary Angles: If the sum of two angles is 180°, these angles are called supplementary angles.
26. Complementary Angles: If the sum of two angles is 90°, then these angles are called complementary angles.
Questions & Answers
Q.1.0) If the measure of angles in a triangle are in the ratio of 2:4:6 , then find all angles of the triangle.
Ans: Let the angles of triangle are 2x,4x,6x , so 2x + 4x + 6x =180°
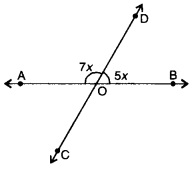
1. In the given figure, AOC is a line, find x. 
2. In the given figure,  intersect at O.
intersect at O.
(a) Determine y, when x = 60°.
(b) Determine x, when y = 40°. 
3. In the given figure, lines Ab, CD and EF intersect at O.
Find the measure of ∠AOC, ∠COF. 
4. The exterior angles obtained on producing the base of a triangle both ways are 100° and 120°. Find all the angles.
5. ΔABC is right angled at A and AL ┴ BC. Prove that ∠BAL = ∠ACD.
6. If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
7. The angles of a triangle are arranged in ascending order of magnitude. If the difference between two consecutive angles is 10°, find all the three angles.
8. In the given figure, POQ is a line. Ray  is another ray lying between rays
is another ray lying between rays  and
and  Prove that
Prove that 
9. Can a triangle have two obtuse angles? Give reason for your answer.
10. How many triangles can be drawn having its angles as 45°, 64° and 72°? Give reason for your answer.
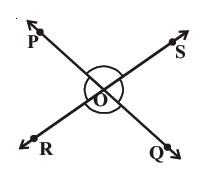
11. In the Fig. lines PQ and RS intersect each other at point O. If ∠POR:∠ROQ=5:7, Find all the angles.
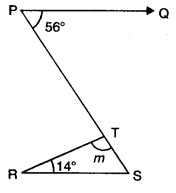
12. If PQ||RS , find value of m.
13. If AB||EF and EF||CD , then find the value of x.

14. In the figure, lines AB and CD intersect at O , Find the value of x.