Heron’s formula, formula credited to Heron of Alexandria (c. 62 CE) for finding the area of a triangle in terms of the lengths of its sides. In symbols, if a, b, and c are the lengths of the sides:  Area = Square root of√s(s - a)(s - b)(s - c)where s is half the perimeter, or (a + b + c)/2.

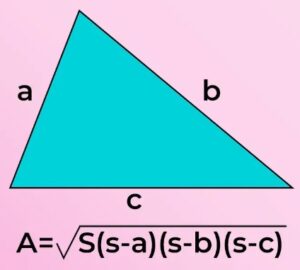
A = √{s(s-a)(s-b)(s-c)}

Where,

• A is area of Triangle ABC,
• a, b, c are lengths of the sides of the triangle, and
• s is semi-perimeter = (a + b + c)/2.

Area of a Triangle = (1/2) × b × h 

Where,

• b is the base, and
• h is the height.

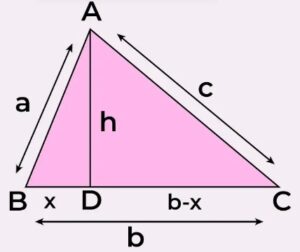
Draw a perpendicular AD on BC

From the ∆ ABD,

a² = x² + h²

⇒ x² = (a²−h²)….(i)

⇒ x = √(a²−h²)….(ii)

Consider the  ∆ACD,

(b−x)² + h² = c²

⇒ (b−x)² = c² − h²

⇒ b² − 2bx + x² = c²–h²

Putting the value of x and x² from equations (i) and (ii) in the above equation, we get

b² – 2b√(a²−h²)+ a²−h² = c² − h²

⇒ b² + a² − c² = 2b√(a² − h²)

Squaring on both sides, we get;

(b² + a² – c²)² = 4b²(a²−h²)

⇒ {(b² + a² – c²)²) / 4b² = (a²−h²)

⇒ a² + {(b² + a² – c²)²) / 4b² = h²

simplifying, we get

h² = (a+b+c)(b+c-a)(a+c-b)(a+b-c) / 4b²

Now, 2s = a+b+c, where s is the semi-perimeter of the triangle.

h² = 2s(2s-2a)(2s-2b)(2s-2c) / 4b²

⇒ h = √[2s(2s-2a)(2s-2b)(2s-2c)] / 2b

⇒ h = 2×√[s(s-a)(s-b)(s-c)] / b…(iii)

From, area of triangle = 1/2 × b × h

Now, area of triangle = 1/2 × {b × 2×√[s(s-a)(s-b)(s-c)]} / b

Area of Triangle (A) = √[s(s-a)(s-b)(s-c)]

Heron’s Formula for Equilateral Triangle

For an equilateral triangle, all sides are equal. Now, the semi-perimeter of the equilateral triangle is

s = (a+a+a) / 2

⇒ s = 3a / 2

where a is the length of the side.

Now, using Heron’s Formula,

Area of Equilateral Triangle = √(s(s – a)(s – a)(s – a)

Area of Equilateral Triangle = √3 / 4 × a²

Heron’s Formula for Scalene Triangle

Area of scalene triangle ABC(A) = √s(s-a)(s-b)(s-c)

Where s is the semi-perimeter i.e., s = (a + b + c)/2.

Heron’s Formula for Isosceles Triangle

rea of iscosceles triangle ABC(A) = √s(s-a)(s-a)(s-b)

Where s is the semi-perimeter i.e., s = (a + b + c)/2.

Simplifying, A = √s(s-a)(s-a)(s-b)

⇒ s = a + b/2

⇒ A = √s(s-a)(s-a)(s-b)

⇒ A = √(a + b/2)(b/2)(b/2)(a – b/2)

⇒ A = √(a + b/2)(a – b/2)(b/2)(b/2)

A = √[(a² – b²/4)(b²/4)]

Solved Examples on Heron’s Formula

Example 1: Calculate the area of a triangle whose lengths of sides a, b, and c are 14cm,13cm, and 15 cm respectively.

Solution:

Given:  

a = 14cm
b = 13cm
c = 15cm

Firstly, we will determine semi-perimeter(s)

s = (a + b + c)/2

⇒ s = (14 + 13 + 15)/2
⇒ s = 21 cm

Thus, A = √(s(s – a)(s – a)(s – a)

⇒ A = √(21(21 – 14)(21 – 13)(21 – 15)

⇒ A = 84 cm²

Example 2: Find the area of the triangle if the length of two sides is 11cm and 13cm and the perimeter is 32cm.

Solution:

Let a, b and c be the three sides of the triangle.

a = 11cm
b= 13 cm

c = ?

Perimeter = 32cm

As we know, Perimeter equals to the sum of the length of three sides of a triangle.

Perimeter = (a + b + c)

⇒ 32 = 11 + 13 + c

⇒ c = 32 – 24

⇒ c= 8 cm

Now as we already know the value of perimeter,

s = perimeter / 2

⇒ s = 32 / 2

⇒ s =16 cm

As, a = 11cm, b = 13 cm, c = 8 cm, s = 16 cm

Thus,  A = √(s(s – a)(s – a)(s – a)

⇒ A = √(16(16 – 11)(16 – 13)(16 – 8)

⇒ A = 43.8 cm²

Example 3: Find the area of an equilateral triangle with a side of 8 cm.

Solution: 

Given,

Side = 8 cm

Area of Equilateral Triangle = √3 / 4 × a²

⇒ Area of Equilateral Triangle = √3 / 4 × (8)²

⇒ Area of Equilateral Triangle = 16 √3 cm²

Important Example: The perimeter of a triangular field is 540 m and its sides are in the ratio 25 : 17 : 12. Find the area of the triangle.

Perimeter of a triangle = 540 m
Ratio in sides = 25:17:12
Sum of ratios = 25+17+12=54