Concepts
- An object is said to be in motion when its position changes with time.
- We describe the location of an object by specifying a reference point. Motion is relative. The total path covered by an object is said to be the distance travelled by it.
- The shortest path/distance measured from the initial to the final position of an object is known as the displacement.
- A Reference Point is used to describe the location of an object. An object can be referred to through many reference points.
- Origin – The reference point that is used to describe the location of an object is called Origin.
- For Example, a new restaurant is opening shortly at a distance of 5 km north of my house. Here, the house is the reference point that is used for describing where the restaurant is located.
What is motion?
If the location of an object changes with time the object is said to be in motion.
Motion in a Straight Line
Distance – The distance covered by an object is described as the total path length covered by an object between two endpoints.
Distance is a numerical quantity. We do not mention the direction in which an object is travelling while mentioning the distance covered by that object.

Figure 1 – Distance and Displacement
According to figure 1 given above, if an object moves from point O to point A then the total distance travelled by the object is given as 60 km.
Displacement – The shortest possible distance between the initial and final position of an object is called Displacement.
Consider figure 1 given above, here the shortest distance between O and A is 60 km only. Hence, displacement is 60 km.
Displacement depends upon the direction in which the object is travelling.
Displacement is denoted by Δx.
| Δx = xf − x0
Where, xf = Final position on the object x0 = Initial position of the object |
Zero Displacement – When the first and last positions of an object are the same, the displacement is zero.
For Example, consider the diagrams given below.

Figure 2 – Example for zero displacement
Displacement at point A = 0 because the shortest distance from A to A is zero.
Negative Displacement and Positive Displacement

Figure 3 – Example for negative and positive displacement
Here, displacement of object B is negative
ΔB = Bf − B0 = 7–12 = – 5
A negative sign indicates the opposite direction here.
Also, displacement of object A is positive
ΔA = Af − A0 = 7– 0 = 7
What are Scalar and Vector Quantities?
- A scalar quantity describes a magnitude or a numerical value.
- A vector quantity describes the magnitude as well as the direction.
- Hence, distance is a scalar quantity while displacement is a vector quantity.
How is distance different from displacement?
| Distance | Displacement |
| Distance provides the complete details of the path taken by the object | Displacement does not provide the complete details of the path taken by the object |
| Distance is always positive | Displacement can be positive, negative or zero |
| It is a scalar quantity | It is a vector quantity |
| The distance between two points may not be unique | Displacement between two points is always unique |
What is uniform motion?
When an object travels equal distances in equal intervals of time the object is said to have a uniform motion.
What is non-uniform motion?
When an object travels unequal distances in equal intervals of time the object is said to have a non-uniform motion.
- The speed of an object is defined as the distance travelled by the object per unit of time.
| SI Unit: Metre (m)
Symbol of Representation: m/s or ms-1 Speed = Distance/Time |

- Average Speed – If the motion of the object is non-uniform then we calculate the average speed to signify the rate of motion of that object.

For Example, If an object travels 10m in 3 seconds and 12m in 7 seconds. Then its average speed would be:
Total distance travelled = 10 m + 12 m = 22m
Total Time taken = 3s + 7s = 10s
Average speed = 22/10 = 2.2 m/s
- To describe the rate of motion in a direction the term velocity is used. It is defined as the speed of an object in a particular direction.
| Velocity = Displacement/Time
SI Unit: Metre (m) Symbol of Representation: M/s or ms-1 |
Average Velocity (in case of uniform motion)-
Average Velocity = (Initial Velocity + Final Velocity)/2
Average Velocity (in case of non-uniform motion)-
Average Velocity = Total Displacement / Total Time taken
What are instantaneous speed and instantaneous velocity?
The magnitude of speed or velocity at a particular instance of time is called Instantaneous Speed or Velocity.

Figure 4 - Instantaneous Speed / Velocity
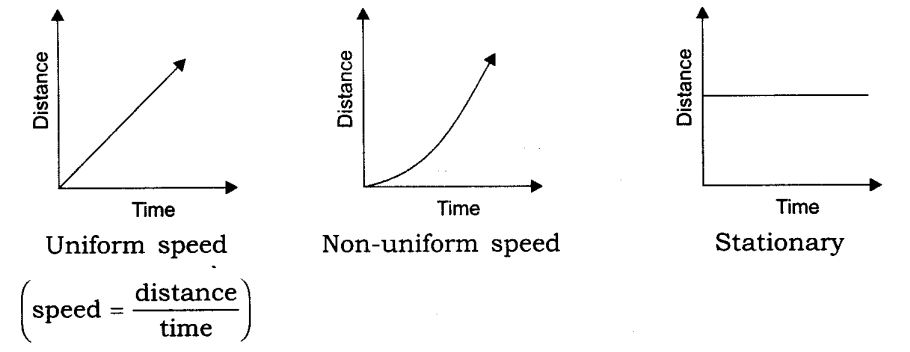
Uniform Motion – In the case of uniform motion the velocity of an object remains constant with change in time. Hence, the rate of change of velocity is said to be zero.
Non-uniform Motion – In the case of non-uniform motion the velocity of an object changes with time. This rate of change of velocity per unit time is called Acceleration.
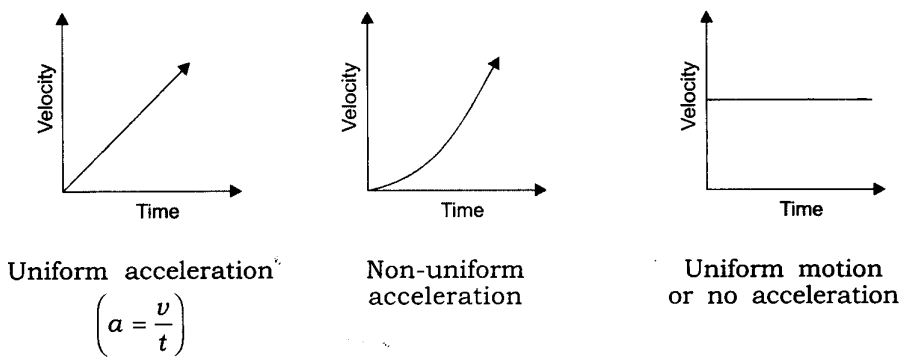
| Acceleration = Change in velocity/ Time taken
SI Unit: m/s2 |
- Uniform motion:When an object covers equal distances in equal intervals of time, it is said to be in uniform motion.
- Non-uniform motion:Motions where objects cover unequal distances in equal intervals of time.
- Speed:The distance travelled by an object in unit time is referred to as speed. Its unit is m/s.
- Average speed:For non-uniform motion, the average speed of an object is obtained by dividing the total distance travelled by an object by the total time taken.
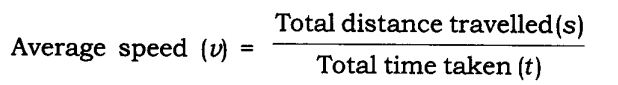
- Velocity: Velocity is the speed of an object moving in definite direction. S.I. unit is m/s.
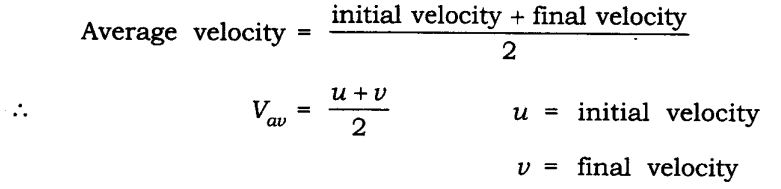
- Acceleration: Change in the velocity of an object per unit time.
![]()
Uniform Acceleration – An object is said to have a uniform acceleration if
- It travels along a straight path
- Its velocity changes (increases or decreases) by equal amounts in equal time intervals
Non - Uniform Acceleration – An object is said to have a non-uniform acceleration if
- Its velocity changes (increases or decreases) by unequal amounts in unequal time intervals
Acceleration is also a vector quantity. The direction of acceleration is the same if the velocity is increasing in the same direction. Such acceleration is called Positive Acceleration.
The direction of acceleration becomes opposite to that of velocity if velocity is decreasing in a direction. Such acceleration is called Negative Acceleration.
De-acceleration or Retardation – Negative acceleration is also called De-acceleration or Retardation
Graphical Representation of Motion
1. Distance – Time Graph
It represents a change in position of the object with respect to time.
The graph in case the object is stationary (means the distance is constant at all time intervals) – Straight line graph parallel to x = axis

Figure 5 - Distance-time Graph in case of Stationary object
The graph in case of uniform motion – Straight line graph

Figure 6 - Distance-time Graph in Uniform Motion
The graph in case of non-uniform motion – Graph has different shapes

Figure 7- Distance-time Graph in Non-Uniform Motion
2. Velocity – Time Graphs
Constant velocity – Straight line graph, velocity is always parallel to the x-axis
Uniform Velocity / Uniform Acceleration – Straight line graph

Non-Uniform Velocity / Non-Uniform Acceleration – Graph can have different shapes

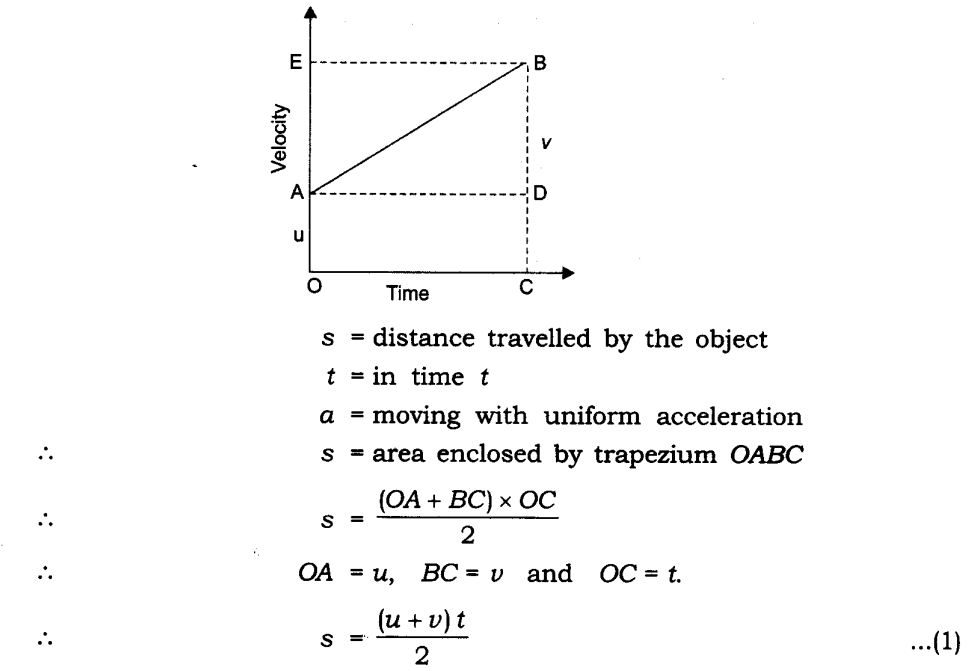
Calculating Displacement from a Velocity-time Graph
Consider the graph given below. The area under the graph gives the distance travelled between a certain interval of time. Hence, if we want to find out the distance travelled between time intervals t1 and t2, we need to calculate the area enclosed by the rectangle ABCD where the area (ABCD) = AB * AC.

Similarly, to calculate distance travelled in a time interval in the case of uniform acceleration, we need to find out the area under the graph, as shown in the figure below.
To calculate the distance between time intervals t1 and t2 we need to find out the area represented by ABED.
Area of ABED = Area of the rectangle ABCD + Area of the triangle ADE = AB × BC + 1/ 2 * (AD × DE)

Equations of Motion
The equations of motion represent the relationship between an object's acceleration, velocity and distance covered if and only if,
- The object is moving on a straight path
- The object has a uniform acceleration
Three Equations of Motion
- The Equation for Velocity – Time Relation
v = u + at
- The Equation for Position – Time Relation
s = ut + 1/2 at2
- The Equation for the Position – Velocity Relation
2a s = v2 – u2
Where
u: initial velocity
a: uniform acceleration
t: time
v: final velocity
s: distance travelled in time t
Deriving the Equations of Motion Graphically

Figure 12
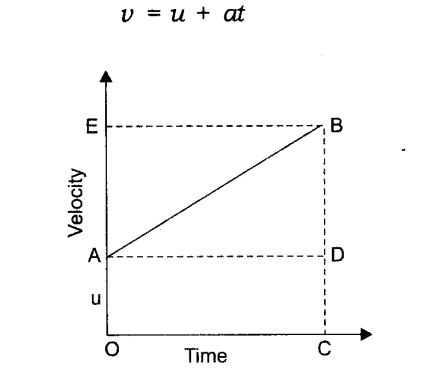
Study the graph above. The line segment PN shows the relation between velocity and time.
Initial velocity, u can be derived from velocity at point P or by the line segment OP
Final velocity, v can be derived from velocity at point N or by the line segment NR
Also, NQ = NR – PO = v – u
Time interval, t is represented by OR, where OR = PQ = MN
1. Deriving the Equation for Velocity – Time Relation
Acceleration = Change in velocity / time taken
Acceleration = (final velocity – initial velocity) / time
a = (v – u)/t
so, at = v – u
v = u + at
2. Deriving Equation for Position – Time Relation
We know that, distance travelled by an object = Area under the graph
So, Distance travelled = Area of OPNR = Area of rectangle OPQR + Area of triangle PQN
s = (OP * OR) + (PQ * QN) / 2
s = (u * t) + (t * (v – u) / 2)
s = ut + 1/2 at2 [because at = v – u]
3. Deriving the Equation for Position – Velocity Relation
We know that, distance travelled by an object = area under the graph
So, s = Area of OPNR = (Sum of parallel sides * height) / 2
s = ((PO + NR)* PQ)/ 2 = ( (v+u) * t)/ 2
2s / (v+u) = t [equation 1]
Also, we know that, (v – u)/ a = t [equation 2]
On equating equations 1 and 2, we get,
2s / (v + u) = (v – u)/ a
2as = (v + u) (v – u)
2 a s = v2 – u2
Uniform Circular Motion
If an object moves in a constant velocity along a circular path, the change in velocity occurs due to the change in direction. Therefore, this is an accelerated motion. Consider the figure given below and observe how the directions of an object vary at different locations on a circular path.

Uniform Circular Motion – When an object travels in a circular path at a uniform speed the object is said to have a uniform circular motion.
Non-Uniform Circular Motion – When an object travels in a circular path at a non-uniform speed the object is said to have a non-uniform circular motion
Examples of uniform circular motion:
- The motion of a satellite in its orbit
- The motion of planets around the sun
Velocity of Uniform Circular Motion
Velocity = Distance/ Time = Circumference of the circle / Time
v = 2πr/ t
where
v: velocity of the object
r: radius of the circular path
t: time taken by the object
(ii) Velocity-time graph
Equation of motion by graphical methods
(i)velocity-time relation:

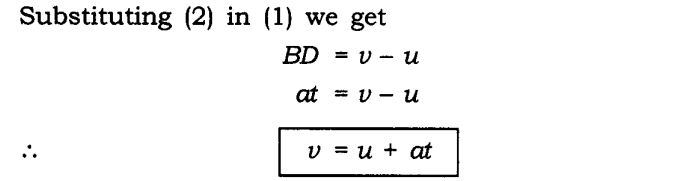
(ii) The equation for position-time relation:

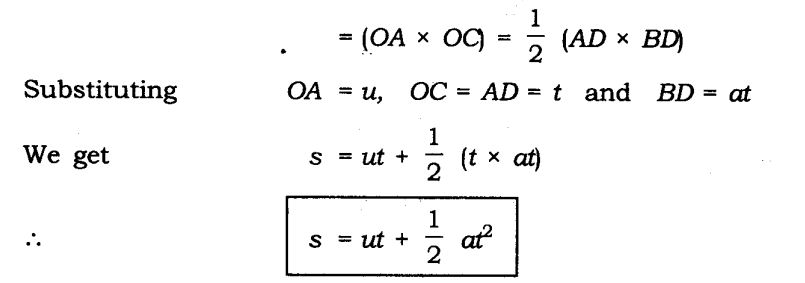
(iii) Equation for position-velocity relation:
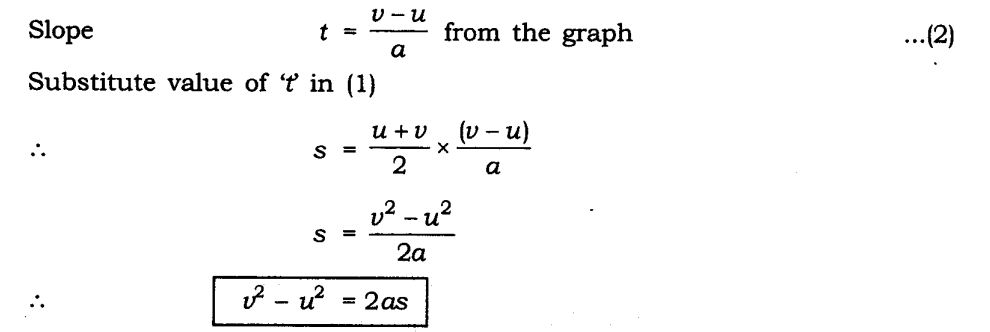
Questions & Answers
Topics covered ( Revised ):
- What is motion?
- Describing motion of a particle
- Position, path length and displacement
- Speed and Velocity
- Rate of change of velocity
- Distance-time graph
- Velocity-time graph
- Equations of Motion
- Uniform Circular Motion
What is motion?
State of Rest: An object is said to be in the state of rest if it does not change its position with respect to time and its surroundings.
State of Motion: An object is said to be in the state of motion if it changes its position with respect to time and its surroundings.
Note: Rest & Motion are relative terms.
Motion can be of different types depending upon the type of path by which the object is going through.
(i) Circulatory motion/Circular motion – In a circular path.

(ii) Linear motion – In a straight line path.

(iii) Oscillatory/Vibratory motion – To and fro path with respect to origin.

Scalar quantity : Physical quantities having magnitude but no direction are called scalars. e.g., distance, speed.
Vector quantity : Physical quantities having both magnitude and direction are called vectors. e.g., displacement, velocity.
Distance (or Path length) & Displacement:

Path length (or distance) : The actual path or length travelled by a object during its journey from its initial position to its final position is called the distance.
Note:
(i) Distance is a scalar quantity which requires only magnitude but no direction.
Example, Manju travelled 65 km.
(ii) Distance is measured by odometer in vehicles.
Displacement: It is the shortest distance between the initial and final position of a object.
Note:
(i) The shortest distance between two point is a straight line.
(ii) Displacement is a vector quantity which requires both magnitude and direction for its explanation.
Example, Nitin travelled 65 km south-west from Clock Tower.
(iii) Displacement can be zero (when initial point and final point of motion are same) Example, circular motion.

Difference between Distance & Displacement:
(1) Distance is the length of actual path travelled by an object whereas displacement is the shortest length between initial and final position of an object.
(2) Distance is a scalar quantity whereas displacement is a vector quantity.
3) Distance remains positive, it cant be zero or negative whereas displacement can be positive, negative or zero.
(4) Distance can be equal to displacement or its greater than displacement whereas displacement can be equal to the distance or its lesser than the distance. It can never be greater than displacement in any situation.
Speed and Velocity
Speed : The measurement of distance travelled by a body per unit time is called speed.
Speed = Distance travelled / Time taken
v= s/t
SI Unit: meter/second (m/s)
Velocity: It is the speed of a body in given direction.
Velocity = Displacement / Time
NOTE:
(1) velocity is a vector quantity. Its value changes when either its magnitude or direction changes.
(2) It can be positive (+ve), negative (-ve) or zero.
Uniform and Non-uniform Motions
Uniform Motion :
When a body travels equal distance in equal interval of time, then the motion is said to be uniform motion.

Non-uniform Motion :
In this type of motion, the body will travel unequal distances in equal intervals of time.

Continuous increase in the slope of curve indicates accelerated motion. The speed of the body is increasing with time.

Continuous decrease in the slope of curve indicates decelerated motion. The speed of the body is decreasing with time.
Non-uniform motion is of two types :
(i) Accelerated Motion : When speed of a body increases with time.

The slope of v-t graph gives acceleration. The slope of the above graph is constant. so the above graph is representing a uniformly accelerated motion.
(ii) De-accelerated Motion : When speed or motion of a body decreases with time.
NOTE:
- If a body is executing uniform motion, then there will be a constant speed.
- If a body is travelling with non-uniform motion, then the speed will not remain uniform but have different values throughout the motion of such body.For non-uniform motion, average speed will describe one single value of speed throughout the motion.
For non-uniform motion, average speed will describe one single value of speed throughout the motion.
Average speed = Total distance travelled / Total time taken
NOTE:
(I) For non-uniform motion in a given line, average velocity will be calculated in the same way as done in average speed.
Average velocity = Total displacement/Total time
(II) For uniformly changing velocity, the average velocity can be calculated as follows :
Average velocity = (Initial velocity + Final velocity)/2
Vaverage = (u + v)/2
where, u = initial velocity, v = final velocity
Acceleration : Acceleration is seen in non-uniform motion and it can be defined as the rate of change of velocity with time.
Acceleration = Change in velocity / Time
a= (v-u)/t
where, v = final velocity, u = initial velocity
If v > u, then ‘a’ will be positive (+ve).
Retardation/Deceleration : Deceleration is seen in non-uniform motion during decrease in velocity with time. It has same definition as acceleration.
Deceleration = Change in velocity / Change in time
a’=(v-u)/t
Here v < u, ‘a’ = negative (-ve).
Equation of Motion (For Uniformly Accelerated Motion)
(i) First Equation:
v = u + at
Final velocity = Initial velocity + Acceleration × Time
Graphical Derivation :
Suppose a body has initial velocity ‘u’ (i.e., velocity at time t = 0 sec.) at point ‘A’ and this velocity changes to ‘v’ at point ‘B’ in ‘t’ secs. i.e., final velocity will be ‘v’.

For such a body there will be an acceleration.

(ii) Second Equation:

Distance travelled by object



(iii) Third Equation:





Uniform Circular Motion:
If a body is moving in a circular path with uniform speed, then it is said to be executing uniform circular motion. In such a motion the speed may be same throughout the motion but its velocity (which is tangential) is different at each and every point of its motion. Thus, uniform circular motion is an accelerated motion.

Example 1: A body travels in a semicircular path of radius 10 m starting its motion from point ‘A’ to point ‘B’. Calculate the distance and displacement.
Solution:
Given,
π=3.14, R=10m
Total distance travelled by the object
distance=πR= 3.14 x 10 = 31.4 m
Total displacement of the body, D=2R = 2 x 10 = 20 m
Example 2. A body travels 4 km towards North then he turn to his right and travels another 4 km before coming to rest. Calculate (i) total distance travelled, (ii) total displacement.
Solution:

Total distance travelled, = OA + AB= 4 + 4 = 8 km
Total displacement=OB=√(OA2+OB2)=√(42+42)=√32=5.65 km
Conversion factor:
1 km/hr = 1000 m / 3600 s =5/18 m/s
Note:
To convert from km/hr to m/s → multiply by 5/18
To convert from m/s to km/hr → multiple by 18/5
Examples:
(1) 72 km/hr = 72 x 5/18 = 20 m/s
(2) 54 km/hr = 54 x 5/18 = 15 m/s
(3) 50 m/s = 50 x 18/5 = 180 km/hr
Solved Examples:
Example : What will be the speed of body in m/s and km/hr if it travels 40 km in 5 hrs ?
Solution :
Distance (s) = 40 km
Time (t) = 5 hrs.
Speed = Total distance / Total time = 40 km/ 5 hrs. = 8 km/hr. (in km/hr)
Speed in m/s:
8 km/hr = 8 x 5/18 = 40/18 = 2.22 m/s
Example 1 : A car speed increases from 40 km/hr to 60 km/hr in 5 sec. Calculate the acceleration of car.
Solution :
Given,
u = 40 km/hr = 40 x 5/18 = 11.11 m/s
v = 60 km/he = 60 x 5/18 = 16.66 m/s
a = ?
We know that,
a=(v-u)/t = (16.66-11.11)/5 = 5.55/5 = 1.11 m/s2
Example 2. A car travelling with a speed of 20 km/hr comes into rest in 0.5 hrs. What will be the value of its retardation ?
Solution :
Given,
v = 0 km/hr
u = 20 km/hr
t = 0.5 hrs.
Retardation, -a = ?
We have,
a =(v-u)/t = (0-20)/0.5 = -40 km/hr2
Therefore, retardation = 40 km/hr2




