Key Concepts
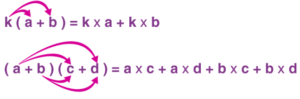
Example: Factorisation of x2 – 4 is (x – 2) (x + 2). It means both (x- 2) and (x + 2) are the factors of x2 – 4.
| 24 = 4 × 6 | 4 and 6 are the factors of 24 |
| 9 = 3 × 3 | 3 is the factor of 9 |
What is a Term?
It is something which is to be added or subtracted (subtracting is adding a negative number) in an expression.
If 2x + 7 is an expression, then 2x and 7 are the terms.
Sum = term + term
What is a Factor?
It is something that is to be multiplied in an expression.
Product = factor × factor
For example :
p = 4(2q – 6)
4 and 2q – 6 are the factors whereas 2q and 6 are the terms.
Basic Factorisation Formula
- a2 – b2 = (a – b)(a + b)
- (a + b)2 = a2 + 2ab + b2
- (a – b)2 = a2 – 2ab + b2
- a3 – b3 = (a – b)(a2 + ab + b2)
- a3 + b3 = (a + b)(a2 – ab + b2)
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
- (a – b – c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ca
Factorisation Methods
There are four methods to factorise the algebraic expressions.
- Common factors method
- Regrouping terms method
- Factorisation using identities
- Factors of the form (x+a) (x+b)
Method of Common Factors
In this method, we simply take out the common factors among each term of the given expression.
Example: Factorise 3x + 9.
Since, 3 is the common factor for both the terms 3x and 9, thus taking 3 as a common factor we get;
Regrouping of Terms Method
Regrouping means rearranging the given expression based on the like terms or similar terms.
For example, 2xy + 3x + 2y + 3 can be rearranged as:
2xy + 3x + 2y + 3
Expanding the terms into factor form.
= 2 × x × y + 3 × x + 2 × y + 3
Rearrange to get the common factor
= x × (2y + 3) + 1 × (2y + 3)
Now (2y + 3) is the common factor we can take out.
= (2y + 3) (x + 1)
Thus, these are the required factors.
Factorisation using identities
By using the common identities, we can factorise the given expression.
Example: Factorise 4x2 – 9.
Solution: By using the algebraic identities, we know;
a2 – b2 = (a – b) (a+b)
Hence, we can write,
4x2 – 9
= (2x)2 – 32
= (2x + 3) (2x – 3)
Note: For the rest identities check with the formulas for factorisation mentioned in the above section.
Factors of the Form (x+a) (x+b)
If a given expression is in the form of x2 + (a + b) x + ab, then the factors will be (x+a) and (x + b).
Example: Factorise x2 + 5x + 6.
Solution: If we compare the given expression with x2 + (a + b) x + ab, then;
a+b = 5 ….(i)
ab = 6 ….(ii)
Now we will try putting the values for a and b such that they satisfy the above two equations.
If we put a = 4 and b = 1, then a + b = 5 satisfies the eq.(i) but a.b = 4, does not satisfy eq.(ii).
Again, if a = 2 and b = 3, then a + b = 5 satisfies eq.(i) but a.b = 6, does not satisfy eq.(ii).
x2 + 5x + 6
= x2 + (2 + 3)x + 2.3
= x2 + 2x + 3x + 2.3
= x(x+2) + 3(x+2)
Factorization Formula for a Quadratic Polynomial
A “quadratic” is a polynomial that is written like “ax2 + bx + c”, where “a”, “b”, and “c” are just numbers. For an easy case of factoring, you can identify the two numbers that will not only multiply to equal the constant term “c” but also add up to equal “b,” the coefficient on the x-term.
Factorising formulas algebra is especially important when solving quadratic polynomial When reducing formulas we normally have to remove all the brackets, but in particular cases, for example with fractional formulas, sometimes we can use factorisation to shorten a formula.
Solved Examples
Here are some maths factorisation example questions and how to factorise the quadratic polynomial are explained in detail.
Q.1: Factorise the Quadratic Polynomial:
x2 + 7x + 6
The constant term is 6, which can be written as the product of 2 and 3 or of 1 and 6. But 2 + 3 = 5, so 2 and 3 are not the numbers I need in this case. On the other hand, 1 + 6 = 7, so you can use 1 and 6:
x2 + 7x + 6 = (x+1)(x+6)
Note that the order doesn’t matter in multiplication, so the above answer can be written as “(x + 6)(x + 1)”.
Q.2: Factorise: x2 – 64.
Solution: Given, x2 – 64
We can also write the given expression as:
⇒ x2 – 82 [Since 8 x 8 = 64]
Now by using the formula,
⇒ a2 – b2 = (a + b) (a – b)
⇒ x2 – 82 = (x + 8) (x – 8)
Q.3: Find the greatest common factor of 6x7 + 3x4 − 9x3.
Solution: Given, 6x7 + 3x4 − 9x3
Now factoring the given expression, we get;
⇒ 3x3 ( 2x4 + x − 3 )
Therefore, the greatest common factor is 3x3.
Q.4: Factorise (7 x + 7 x3) + (x4 + x6).
Solution: (7 x + 7 x3) + (x4 + x6)
Open all the brackets.
⇒ 7x + 7x3 + x4 + x6
Taking the common factors.
⇒ 7x (1 + x2) + x4 (1 + x2)
⇒ (7x + x4) (1 + x2)
⇒ x (7 + x3 ) (1 + x2)
Practice Questions
- Factorise 10x2 + x – 2. [Answer: (5x – 2)(2x + 1)]
- Factorise 4x2 + 12x + 5. [Answer: (2x + 5)(2x + 1)]
- Factor the polynomial x2 – 10x + 21 [Answer: (x – 3) (x – 7)]

