Key Concepts
The exponent of a number says how many times to use the number in a multiplication.
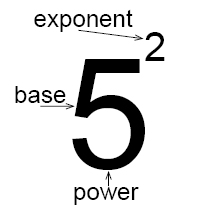
In 52 the "2" says to use 5 twice in a multiplication, so 52 = 5 × 5 = 25
So in general:
| an tells you to multiply a by itself, so there are n of those a's: |
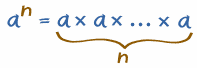 |
Another Way of Writing It
Example: 2^4 is the same as 24
2^4 = 2 × 2 × 2 × 2 = 16
Negative Exponents
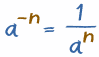 |
Example: 8-1 = 18 = 0.125
Example: 5-3 = 15 × 15 × 15 = 0.008
More Examples:
| Negative Exponent | Reciprocal of Positive Exponent |
Answer | ||
|---|---|---|---|---|
| 4-2 | = | 1 / 42 | = | 1/16 = 0.0625 |
| 10-3 | = | 1 / 103 | = | 1/1,000 = 0.001 |
| (-2)-3 | = | 1 / (-2)3 | = | 1/(-8) = -0.125 |
What if the Exponent is 1, or 0?
| 1 | If the exponent is 1, then you just have the number itself (example 91 = 9) | |
| 0 | If the exponent is 0, then you get 1 (example 90 = 1) | |
| But what about 00 ? It could be either 1 or 0, and so people say it is "indeterminate". |
Be Careful About Grouping
To avoid confusion, use parentheses () in cases like this:
| With () : | (−2)2 = (−2) × (−2) = 4 |
| Without () : | −22 = −(22) = −(2 × 2) = −4 |
| With () : | (ab)2 = ab × ab |
| Without () : | ab2 = a × (b)2 = a × b × b |
Let ‘a’ is any number or integer (positive or negative) and ‘m’, ‘n’ are positive integers, denoting the power to the bases, then;
Multiplication Law
As per the multiplication law of exponents, the product of two exponents with the same base and different powers equals to base raised to the sum of the two powers or integers.
am × an = am+n
Division Law
When two exponents having same bases and different powers are divided, then it results in base raised to the difference between the two powers.
am ÷ an = am / an = am-n
Rules of Exponents
The rules of exponents are followed by the laws. Let us have a look at them with a brief explanation.
Suppose ‘a’ & ‘b’ are the integers and ‘m’ & ‘n’ are the values for powers, then the rules for exponents and powers are given by:
i) a0 = 1
As per this rule, if the power of any integer is zero, then the resulted output will be unity or one.
Example: 50 = 1
ii) (am)n = a(mn)
‘a’ raised to the power ‘m’ raised to the power ‘n’ is equal to ‘a’ raised to the power product of ‘m’ and ‘n’.
Example: (52)3 = 52 x 3
iii) am × bm =(ab)m
The product of ‘a’ raised to the power of ‘m’ and ‘b’ raised to the power ‘m’ is equal to the product of ‘a’ and ‘b’ whole raised to the power ‘m’.
Example: 52 × 62 =(5 x 6)2
iv) am/bm = (a/b)m
The division of ‘a’ raised to the power ‘m’ and ‘b’ raised to the power ‘m’ is equal to the division of ‘a’ by ‘b’ whole raised to the power ‘m’.
Example: 52/62 = (5/6)2
v) (-1)odd no. = -1 ; (-1)even no. = 1 ;
vi) A number expressed in the form of P x 10n is called scientific notation or standard form of exponents. Where P is a terminating decimal and 1 < P < 10.
Fractional Exponents
x1/n = The n-th Root of x
A fractional exponent like 1/n means to take the n-th root:
x1/n = n√x
| An exponent of 1/2 is a square root
An exponent of 1/3 is a cube root An exponent of 1/4 is a 4th root And so on! |
 |
Answer: 271/3 = 3√27 = 3
A fractional exponent like m/n means:
Some examples:
Example: What is 43/2 ?
43/2 = 43×(1/2) = √(43) = √(4×4×4) = √(64) = 8
or
43/2 = 4(1/2)×3 = (√4)3 = (2)3 = 8
Either way gets the same result.
Example: What is 274/3 ?
274/3 = 274×(1/3) = 3√274 = 3√531441 = 81
or
274/3 = 27(1/3)×4 = (3√27 )4 = (3)4 = 81
It was certainly easier the 2nd way!
Mock Test
Write answers of below questions:
- Simplify 253/53
- The value of 2-4
- The value of (4/3)-2
- The value of ((3)-2)-2
- Simplify (50+ 40) x )-1
- 0.00024 in standard form will be
- Identify the exponent and power for the expression 48
- The value of 274/3
- The value of (625)1/4
-
Find the value of:
Submit your answers here:

