• A fraction shows part of a whole. This whole can be a region or a collection or a group.

 

 

 

 

 

 

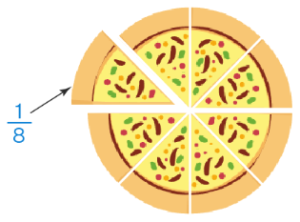
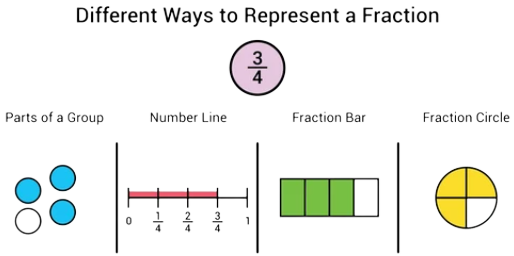
Parts of a Fraction

• All fractions consist of a numerator and a denominator and they are separated by a horizontal bar known as the fractional bar.
• The denominator indicates the number of parts in which the whole has been divided into. It is placed in the lower part of the fraction below the fractional bar.
• The numerator indicates how many sections of the fraction are represented or selected. It is placed in the upper part of the fraction above the fractional bar.

Based on the numerator and denominator, which are parts of a fraction, there are different types of fractions as listed below:

• Proper Fraction :Proper fractions are the fractions in which the numerator is less than its denominator. For example, 5/7, 3/8, 2/5, and so on are proper fractions.
• Improper Fraction :An improper fraction is the type of fraction in which the numerator is more than or equal to its denominator. It is always the same or greater than the whole. For example, 4/3, 5/2, 8/5, and so on.
• Unit Fraction :Fractions in which the numerator is 1 are known as unit fractions. For example, 1/4, 1/7, 1/9, and so on.
• Mixed Fraction: A mixed fraction is a mixture of a whole number and a proper fraction. For example, $5\frac{1}{3}$, where 5 is the whole number and 1/3 is the proper fraction, or, $2\frac{2}{5}$, $7\frac{9}{11}$, and so on.

• Equivalent Fraction :Equivalent fractions are the fractions that represent the same value after they are simplified.

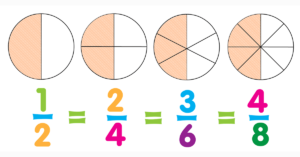
• To get equivalent fractions of any given fraction:
  • We can multiply both the numerator and the denominator of the given fraction by the same number.
  • We can divide both the numerator and the denominator of the given fraction by the same number.
  • Example: Find the two fractions that are equivalent to 5/7. Solution: Equivalent Fraction 1: Let us multiply the numerator and the denominator with the same number 2. This means, 5/7= (5 × 2)/(7 × 2) = 10/14
  • Equivalent Fraction 2: Let us multiply the numerator and the denominator with the same number 3. This means, 5/7 = (5 × 3)/(7 × 3) = 15/21. Therefore, 10/14, 15/21, and 5/7 are equivalent fractions.
• Like Fractions: Like fractions are the fractions that have the same denominators. For example, 5/15, 3/15, 17/15, and 31/15 are like fractions.
• Unlike Fractions :Unlike fractions are the fractions which have different denominators. For example, 2/7, 9/11, 3/13, and 39/46 are unlike fractions.

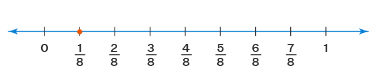
The representation of fractions on a number line demonstrates the intervals between two integers, which also shows us the fundamental principle of fractional number creation. The fractions on a number line can be represented by making equal parts of a whole, i.e., from 0 to 1. The denominator of the fraction would represent the number of equal parts in which the number line will be divided and marked. For example, if we need to represent 1/8 on the number line, we need to mark 0 and 1 on the two ends and divide the number line into 8 equal parts. Then, the first interval can be marked as 1/8. Similarly, the next interval can be marked as 2/8, the next one can be marked as 3/8, and so on. It should be noted that the last interval represents 8/8 which means 1. Observe the following number line that represents these fractions on a number line.

Adding Fractions

The addition of fractions is easy when they have a common denominator.

For example, ⅔ + 8/3 = (2+8)/3 = 10/3

Hence, we need to just add the numerators here.

Subtracting Fractions

The rule for subtracting two or more fractions is the same as for addition. The denominators should be common to subtract two fractions.

Example: 9/2 – 7/2 = (9-7)/2 = 2/2 = 1

Subtracting with Different Denominators

If the denominators of the two fractions are different, we have to simplify them by finding the LCM of denominators and then making it common for both fractions.

Example: ⅔ – ¾

The two denominators are 3 and 4

Hence, LCM of 3 and 4 = 12

Therefore, multiplying ⅔ by 4/4 and ¾ by 3/3, we get;

8/12 – 9/12

= (8-9)/12

= -1/12

Multiplication of Fractions

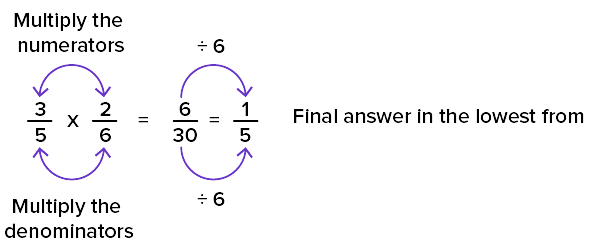
When two fractions are multiplied, then the top part (numerators) and the bottom part (denominators) are multiplied together.

If a/b and c/d are two different fractions, then the multiplication of a/b and c/d will be:

(a/b) x (c/d) = (axc)/(bxd) = (ac/bd)

Two numbers whose product is 1 are called reciprocals.

Another word  for reciprocal is multiplicative inverse.

Example: Multiply ⅔ and 3/7.

(⅔) x (3/7) = (2×3)/(3×7) = 2/7

Division of Fractions

While dividing with fractions always find the reciprocal only of the divisor.

If a/b and c/d are two different fractions, then the division a/b by c/d can be expressed as:

(a/b)÷(c/d) = (a/b)x(d/c) = (ad/bc)

Example: Divide ⅔ by 3/7.

(⅔) ÷ (3/7) = (⅔) x (7/3) = (2×7)/(3×3) = 14/9

How to Convert Fractions To Decimals?

As we already learned enough about fractions, which are part of a whole. The decimals are the numbers expressed in a decimal form which represents fractions, after division.

For example, Fraction 1/2 can be written in decimal form as 0.5.

The best part of decimals are they can be easily used for any arithmetic operations such as addition, subtraction, etc. Whereas it is difficult sometimes to perform operations on fractions. Let us take an example to understand;

Example: Add 1/6 and 1/4.

solution: 1/6 = 0.17 and 1/4 = 0.25

Hence, on adding 0.17 and 0.25, we get;

0.17 + 0.25 = 0.42

How to Simplify Fractions?

To simplify the fractions easily, first, write the factors of both numerator and denominator. Then find the largest factor that is common for both numerator and denominator. Then divide both the numerator and the denominator by the greatest common factor (GCF) to get the reduced fraction, which is the simplest form of the given fraction. Now, let us consider an example to find the simplest fraction for the given fraction.

For example, take the fraction, 16/48

So, the factors of 16 are 1, 2, 4, 8, 16.

Similarly, the factors of 48 are 1, 2, 3, 4, 6, 8, 12, 16, 24, 48.

Thus, the greatest common factor for 16 and 48 is 16.

i.e. GCF (16, 48) = 16.

Now, divide both the numerator and denominator of the given fraction by 16, we get

16/48 = (16/16) / (48/16) = 1/3.

Hence, the simplest form of the fraction 16/48 is 1/3.

Solved Examples on Fractions

Example 1:

Is 12/6 a fraction?

Solution:

Yes, it is. It is called an improper fraction.

Example 2:

Convert 130.1200 into a fraction.

Solution:

Here will use the concept of how to convert decimals into fractions

130.1200 = 130.1200/10000

= 13012/100

Example 3:

Add 3/ 5 and 10/15.

Solution:

3 /5 + 10/15

LCM of 5 and 15 is 15

= (9 + 10)/15

= 19/15

Example 4:

Which of the following fraction is the largest?

(a) 29/23

(b) 29/27

(c) 29/25

(d) 29/30

Solution:

To find whether the largest fractions among the given options, first convert the fractional value to the decimal value.

(a) 29/23 = 1.261

(b) 29/27 = 1.074

(c) 29/25 = 1.16

(d) 29/30 = 0.967

Thus, 29/23 is the largest fraction among the given options.

Hence, option (a) 29/23 is the correct answer.

Example 5: 

Reduce the fraction 15/65 to the simplest form.

Solution:

Given fraction: 15/65.

Factors of 15: 1, 3, 5 and 15

Factors of 65: 1, 5, 13, and 65

Hence, the greatest common factor of 15 and 65 is 5.

i.e. GCF (15, 65) = 5.

Now, divide both the numerator and the denominator of the given fraction (16/65) by 5, we get

15/65 = (15/5) / (65/5) = 3/13.

Hence, the simplest form of the fraction 15/65 is 3/13.