Question 1: Given here are some figures.

   

Classify each of them on the basis of the following.
(a) Simple curve (b) Simple closed curve (c) Polygon (d) Convex polygon (e) Concave polygon

Solution:

(a) Simple curve: 1, 2, 5, 6, 7
(b) Simple closed curve: 1, 2, 5, 6, 7
(c) Polygon: 1, 2
(d) Convex polygon: 2
(e) Concave polygon: 1

Question 2: How many diagonals does each of the following have?

(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle

Solution: (a) Two, (b) 9, (c) 0 (zero)

Question 3: What is the sum of the measures of the angles of a convex quadrilateral? Why this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try!)

Solution: Angle sum of a convex quadrilateral $=(4–2)\times 180⁰=2\times 180⁰=360⁰$
Since, quadrilateral, which is not convex, i.e. concave has same number of sides i.e. 4 as a convex quadrilateral have, thus, a quadrilateral which not convex also hold this property. i.e. angle some of a concave quadrilateral is also equal to 360⁰

Question 4: Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)

   

What can you say about the angle sum of a convex polygon with number of sides?
(a) 7

Solution: Given number of sides = 7
Angle sum of a polygon with 7 sides $=(7–2)\times 180⁰=5\times 180⁰=900⁰$

(b) 8

Solution: Given number of sides = 8
Angle sum of a polygon with 8 sides $=(8–2)\times 180⁰=6\times 180⁰=1080⁰$

(c) 10

Solution: Given number of sides = 10
Angle sum of a polygon with 10 sides $=(10–2)\times 180⁰=8\times 180⁰=1440⁰$

(d) n

Solution: Given number of sides = n
Angle sum of a polygon with n sides $=(n–2)\times 180⁰=(n–2)180⁰$

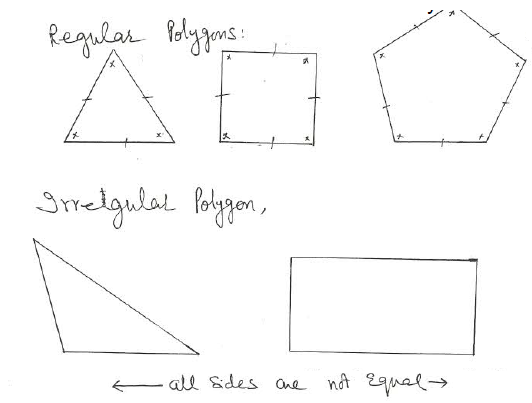
Question 5: What is a regular polygon?
State the name of a regular polygon of (i) 3 sides (ii) 4 sides (iii) 6 sides

Solution: A polygon with equal sides and equal angles is called reagular polygon.
(i) Equilateral triangle
(ii) Square
(iii) Regular hexagon

Question 6: Find the angle measures x in the following figures.

Solution: We know that, angle sum of a quadrilateral = 360⁰
So, $50°+130°+120°+x=360°$
Or, $300°+x=360°$
Or, $x=360°-300°=60°$

Question 6 (b)

Solution:

We know that, angle sum of a quadrilateral = 360⁰
So, $90°+60°+70°+x=360°$
Or, $220°+x=360°$
Or, $x=360°-220°=140°$

Question 6 (c)

Solution:

We know that angle sum of a pentagon = 540^o
$110°+120°+30°+x+x=540°$
Or, $260°+2x=540°$
Or, $2x=540°-260°=280°$
Or, $x=280°÷2=140°$

Question 6 (d)

Solution:Angle sum of a pentagon $=(5–2)\times 180⁰=3\times 180⁰=540⁰$
Since, it is a regular pentagon, thus, its angles are equal
So, $x+x+x+x+x=540°$
Or, $5x=540°$
Or, $x=540°÷5=108°$

Question 7:

Solution:

We know that angle sum of a triangle = 180⁰
Thus, $30⁰+90⁰+C=180⁰$
Or, $120⁰+C=180⁰$
Or, $C=180⁰–120⁰$
Or, $C=60⁰$
Now, $y=180°-C$
Or, $y=180°-60°=120°$
Similarly, $z=180°-30°=150°$
Similarly, $x=180°-90°=90°$
Hence, $x+y+z=90°+120°+150°=360°$

Alternate method: We know that sum of external angles of a polygon = 360⁰
Hence, $x+y+z=180°$

Solution:

We know that angle sum of a quadrilateral = 360⁰
$A+60°+80°+120°=360°$
Or, $A+260°=360°$
Or, $A=360°-260°=100°$
Hence, $w=180°-100°=80°$
Similarly, $x=180°-120°=60°$
Similarly, $y=180°-80°=100°$
Similarly, $z=180°-60°=120°$
Hence, $x+y+z+w=60°+100°+120°+80°=360°$

Alternate method: We know that sum of external angles of a polygon = 360⁰
Hence, $x+y+z+w=360°$

Question 8: Find x in the following figures.

Solution: We know that sum of exterior angles of a polygon = 360⁰
So, $125°+125°+x=360°$
Or, $250°+x=360°$
Or, $x=360°=250°=110°$

Solution:

We know that sum of exterior angles of a polygon = 360⁰
So, $70°+x+90°+60°+90°=360°$
Or, $310°+x=360°$
Or, $x=360°-310°=50°$

Question 9: Find the measure of each exterior angle of a regular polygon of

(i) 9 sides

Solution: Since, 9 sides of a polygon has nine angles
And we know that sum of exterior angles of a polygon = 360⁰
So, 9 exterior angles = 360°
Or, 1 exterior angle $=360°÷9=40°$

(ii) 15 sides

Solution: Since, 15 sides of a polygon has 15 angles
And we know that sum of exterior angles of a polygon = 360⁰
So, 15 exterior angles = 360°
Or, 1 exterior angle $=360°÷15=24°$

Question 10: How many sides does a regular polygon have if the measure of an exterior angle is 24⁰?

Solution: We know that number of angles of a polygon = number of sides
And we know that sum of exterior angles of a polygon = 360⁰
So, measure of each angle = 24°
Or, number of exterior angles $=360°÷24°=15$
Hence, number of sides = 15

Question 11: How many sides does a regular polygon have if each of its interior angles is 165⁰?

Solution: Here, each interior angle = 165°
Hence, each exterior angle = 180° - 165° = 15°
As, measure of each exterior angle = 15°
So, number of sides $=360°÷15°=24$
Hence, number of sides = 24

Question 12: (a) Is it possible to have regular polygon with measure of each exterior angle as 22⁰?

Solution:
Since, number of sides of a polygon = 360° ÷ each exterior angle
Hence, number of sides of given polygon $=360°÷22°=16.36$

Since, answer is not a whole number, thus, a regular polygon with measure of each exterior angle as 22⁰ is not possible.
Hence, Answer = no

(b) Can it be an interior angle of a regular polygon? Why?

Solution: Here, each interior angle = 22°
Hence, each exterior angle $=180°-22°=158°$
Hence, number of sides $=360°÷158°=2.27$

Since, answer is not a whole number, thus, a regular polygon with measure of each interior angle as 22⁰ is not possible.
Hence, Answer = no

Question 13: (a) What is the minimum interior angle possible for a regular polygon? Why?

Solution: Triangle is the polygon with minimum number of sides and an equilateral triangle is a regular polygon because all sides are equal in this. We know that each angle of an equilateral triangle measures 60 degree. Hence, 60 degree is the minimum possible value for internal angle of a regular polygon.

(b) What is the maximum exterior angle possible for a regular polygon?

Solution: Each exterior angle of an equilateral triangle is 120 degree and hence this the maximum possible value of exterior angle of a regular polygon. This can also be proved by another principle; which states that each exterior angle of a regular polygon is equal to 360 divided by number of sides in the polygon. If 360 is divided by 3, we get 120.

Question 14: Given a parallelogram ABCD. Complete each statement along with the definition or property used.

Answer: (a) AD = Opposite Sides are equal
(b) Angle DCB = Opposite angles are equal
(c) OC = Diagonals bisect each other
(d) Angle DAB + angle CDA = 180°

Question 15: Consider the following parallelograms. Find the values of the unknowns x, y, z.

(i)

Solution: Here, $x=180°-100°=80°$
As opposite angles are equal in a parallelogram
So, $y=100°$ and $z=80°$

(ii)

Solution: x, y and z will be complementary to 50°.
So, Required angle $=180°-50°=130°$

(iii)

Solution: z being opposite angle= 80°
x and y are complementary, x and y
$=180°-80°=100°$

(iv)

Solution: As angles on one side of a line are always complementary
So, $x=90°$
So, $y=180°-(90°+30°)=60°$
The top vertex angle of the above figure $=60°\times 2=120°$
Hence, bottom vertex Angle = 120° and
$z=60°$

(v)

Solution: y= 112°, as opposite angles are equal in a parallelogram
As adjacent angles are complementary so angle of the bottom left vertex
$=180°-112°=68°$
So, $z=68°-40°=28°$

Another way of solving this is as follows:
As angles x and z are alternate angles of a transversal so they are equal in measurement.

16. Can a quadrilateral ABCD be a parallelogram if

(i) Angle D + angle B = 180°?
(ii) AB = DC = 8 cm, AD = 4 cm and BC 4.4 cm?
(iii) Angle A = 70° and angle C = 65° ?

Solution: (i)It can be , but not always as you need to look for other criteria as well.
(ii) In a parallelogram opposite sides are always equal, here AD BC, so its not a parallelogram.
(iii) Here opposite angles are not equal, so it is not a parallelogram.

Question 17: The measures of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.

Solution: Opposite angles of a parallelogram are always add upto 180°.
So, $180°=3x+2x$
Or, $5x=180°$
Or, $x=36°$
So, angles are; $36°\times 3=108°$
And $36°\times 2=72°$

Question 18: Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Solution: 90°, as they add up to 180°

Question 19: The adjacent figure HOPE is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.

Solution: Angle opposite to $y=180°-70°=110°$
Hence, $y=110°$
$x=180°-(110°+40°)=30°$, (triangle’s angle sum)
$z=30°$ (Alternate angle of a transversal)

Question 20: The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)

Solution As opposite sides are equal in a parallelogram
So, $3y–1=26$
Or, $3y=27$
Or, $y=9$
Similarly, $3x=18$
Or, $x=6$

Solution: As you know diagonals bisect each other in a parallelogram.
So, $y+7=20$
Or, $y=20–7=13$
Now, $x+y=16$
Or, $x+13=16$
Or, $x=16–13=3$

Question 21: In the given figure both RISK and CLUE are parallelograms. Find the value of x.

Solution: In parallelogram RISK
$\angle ISK=180°-120°=60°$
Similarly, in parallelogram CLUE
$\angle CEU=180°-70°=110°$
Now, in the triangle
$x=180°-(110°-60°)=10°$

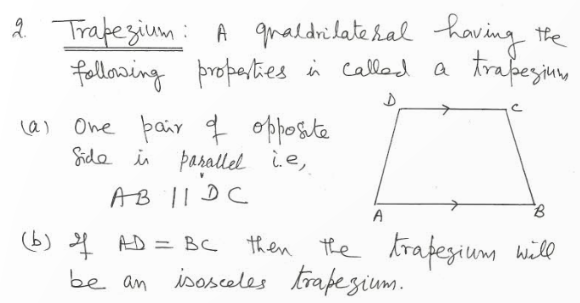
Question 22: Explain how this figure is a trapezium. Which of its two sides are parallel?

Answer: Sum of internal angles on side of transversal ML is 180°. So, SM||KL. Since two sides are parallel, so this is a trapezium.

Question 23: In the given figure, find ∠C if AB||DC

Answer: AB||DC, so sum of internal angles on one side of transversal BC = 180°

Or, ∠C + 120° = 180°

Or, ∠C = 180° - 120° = 60°

Question 24: In the given figure, find the measure of ∠P and ∠S if SP||RQ.

Answer: SP||RQ, so, ∠S = ∠R = 90°

Sum of internal angles of quadrilateral PQRS = 360°

Or, ∠P + 90° + 90° + 130° = 360°

Or, ∠P + 310° = 360°

Or, ∠P = 360° - 30° = 50°

Question 25: State whether True or False.

(a) All rectangles are squares

Answer: All squares are rectangles but all rectangles can’t be squares, so this statement is false.

(b) All kites are rhombuses.

Answer: All rhombuses are kites but all kites can’t be rhombus.

(c) All rhombuses are parallelograms

Answer: True

(d) All rhombuses are kites.

Answer: True

(e) All squares are rhombuses and also rectangles

Answer: True; squares fulfill all criteria of being a rectangle because all angles are right angle and opposite sides are equal. Similarly, they fulfill all criteria of a rhombus, as all sides are equal and their diagonals bisect each other.

(f) All parallelograms are trapeziums.

Answer: False; All trapeziums are parallelograms, but all parallelograms can’t be trapezoid.

(g) All squares are not parallelograms.

Answer: False; all squares are parallelograms

(h) All squares are trapeziums.

Answer: True

Question 2: Identify all the quadrilaterals that have.

(a) four sides of equal length (b) four right angles

Answer: (a) If all four sides are equal then it can be either a square or a rhombus.
(b) All four right angles make it either a rectangle or a square.

Question 26: Explain how a square is.
(i) a quadrilateral (ii) a parallelogram (iii) a rhombus (iv) a rectangle

Answer: (i) Having four sides makes it a quadrilateral
(ii) Opposite sides are parallel so it is a parallelogram
(iii) Diagonals bisect each other so it is a rhombus
(iv) Opposite sides are equal and angles are right angles so it is a rectangle.

Question 27: Name the quadrilaterals whose diagonals.
(i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal

Answer: Rhombus; because, in a square or rectangle diagonals don’t intersect at right angles.

Question 28: Explain why a rectangle is a convex quadrilateral.

Answer: Both diagonals lie in its interior, so it is a convex quadrilateral.

Question 29: ABC is a right-angled triangle and O is the mid point of the side opposite to the right angle. Explain why O is equidistant from A, B and C.

Answer: If we extend BO to D, we get a rectangle ABCD. Now AC and BD are diagonals of the rectangle. In a rectangle diagonals are equal and bisect each other.
So, AC = BD
AO = OC
BO = OD
And AO = OC = BO = OD
So, it is clear that O is equidistant from A, B and C.

Question 30: Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $60°+35°+x=180°$
Or, $95°+x=180°$
Or, $x=180°-95°=85°$

Question 31: Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $65°+45°+x=180°$
Or, $110°+x=180°$
Or, $x=180°-110°-70°$

Question 32: Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $62°+74°+x=180°$
Or, $136°+x=180°$
Or, $x=180°-136°=44°$

Question 33: Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $62°+72°+x=180°$
Or, $139°+x=180°$
Or, $x=180°-139°=41°$

Question 34 Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $84°+55°x=180°$
Or, $139°+x=180°$
Or, $x=180°-139°=41°$

Question 35: Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $35°+x+x=180°$
Or, $35°+2x=180°$
Or, $2x=180°-35°=145°$
Or, $x=145°÷2=72.5°$

Question 36: Find the angle x

Answer: We know that, angle sum of a triangle = 180⁰
So, $30°+x+x=180°$
Or, $30°+2x=180°$
Or, $2x=180°-30°=150°$
Or, $x=150°÷2=75°$

Question 37: Find the angle y

Answer: We know that, angle sum of a triangle = 180⁰
So, $27°+x+x=180°$
Or, $27°+2x=180°$
Or, $2x=180°-27°=153°$
Or, $x=153°÷2=76.5°$

Question 38: Find the angle y

Answer: We know that, angle sum of a triangle = 180⁰
So, $90°+y+y=180°$
Or, $90°+2y=180°$
Or, $2y=180°=90°$
Or, $y=90°÷2=45°$

Question 39: Find the angle y

Answer: We know that, angle sum of a triangle = 180⁰
So, $y+y+y=180°$
Or, $3y=180°$
Or, $y=180°÷3=60°$

Question 40: Find the angle y

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $85°+95°+100°+y=360°$
Or, $280°+y=360°$
Or, $y=360°-280°=80°$

Question 41: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $95°+75°+110°+x=360°$
Or, $280°+x=360°$
Or, $x=360°-280°=80°$

Question 42: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $65°+120°+90°+x=360°$
Or, $275°+x=360°$
Or, $x=360°-275°=85°$

Question 43: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $65°+70°+120°+x=360°$
Or, $255°+x=360°$
Or, $x=360°-255°=105°$

Question44: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
Or, $185°+2x=360°$
Or, $2x=360°-185°=175°$
Or, $x=175°÷2=87.5°$

Question 45: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $95°+115°+x+x=360°$
Or, $210°+2x=360°$
Or, $2x=360°-210°=150°$
Or, $x=150°÷2=75°$

Question 46: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $120°+x+x+x=360°$
Or, $120°+3x=360°$
Or, $3x=360°-120°=240°$
Or, $x=240°÷3=80°$

Question 47: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $84°+x+x+x=360°$
Or, $84°+3x=360°$
Or, $3x=360°-84°=276°$
Or, $x=276°÷3=92°$

Question 48: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
So, $90°+x+x+x=360°$
Or, $90°+3x=360°$
Or, $3x=360°-90°=270°$
Or, $x=270°÷3=90°$

Question 49: Find the angle x

Answer: We know that angle sum of a quadrilateral = 360⁰
Or, $4x=360°$
Or, $x=360°÷4=90°$

Question 50: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $110°+90°+120°+85°+x=540°$
Or, $405°+x=540°$
Or, $x=540°-405°=135°$

Question 51: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $120°+90°+135°+98°+x=540°$
Or, $443°+x=540°$
Or, $x=540°-443°=97°$

Question 52: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $125°+87°+115°+105°+x=540°$
Or, $432°+x=540°$
Or, $x=540°-432°=108°$

Question 53: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $125°+87°+110°+x+x=540°$
Or, $322°+2x=540°$
Or, $2x=540°-322°=218°$
Or, $x=218°÷2=109°$

Question 54: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $125°+90°+105°+x+x=540°$
Or, $320°+2x=540°$
Or, $2x=540°-320°=220°$
Or, $x=220°÷2=110°$

Question 55: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $115°+115°+90°+x+x=540°$
Or, $320°+2x=540°$
Or, $2x=540°-320°=220°$
Or,  $x=220°÷2=110°$

Question 56: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $120°+90°+x+x+x=540°$
Or, $210°+3x=540°$
Or, $3x=540°-210°=330°$
Or, $x=330°÷3=110°$

Question 57: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $90°+x+x+x+x=540°$
Or, $90°+4x=540°$
Or, $4x=540°-90°=450°$
Or, $x=450°÷4=112.5°$

Question 58: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $120°+x+x+x+x=540°$
Or, $120°+4x=540°$
Or, $4x=540°-120°=420°$
Or, $x=420°÷4=105°$

Question 59: Find the angle x

Answer: We know that angle sum of pentagon = 540⁰
So, $x+x+x+x+x=540°$
Or, $5x=540°$
$x=540°÷5=108°$