Linear Equations in One Variable – Hari Shanker Pandey Sewa Samiti

Concepts

Understand fundamentals

Linear equation in one variable is the basic equation used to represent and solve for an unknown quantity. Another way to recognize a linear equation is to note that it has only one variable and the highest degree of the variable is 1)
It can be easily represented graphically and it is always a straight line. The general form of a linear equation in one variable is Ax + B = 0. Here A is the coefficient of x, x is the variable, and B is the constant term. The coefficient and the constant term should be segregated to find the final solution of this linear equation.

For Example : 3x + 7 = 12, is equation in one variable x. 2x + 3y = 15, are equations in two variables x and y.

Rules for Solving Linear Equations in One Variable
We learnt the rules for solving an equation in one variable. Let us recall them. They are :
Rule 1 : Same quantity (number) can be added to both sides of an equation without changing the equality.
Rule 2 : Same quantity can be subtracted from both sides of an equation without changing the equality.
Rule 3 : Both sides of an equation may be multiplied by the same non-zero number without changing the equality.
Rule 4 : Both sides of an equation may be divided by the same non-zero number without changing the equality. It should be noted that some complicated equations can be solved by using two or more of these rules together.

For solving an equation having only one variable, the following steps are followed

Step 1: Using LCM, clear the fractions if any.
Step 2: Simplify both sides of the equation.
Step 3: Isolate the variable.
Step 4: Verify your answer.

Q1:

Q3 : Amina thinks of a number and subtracts 5/2 from it. She multiplies the result by 8. The result now obtained is 3 times the same number she thought of. What is the number?
Solution:
Let the required number be x.
Condition I: x – 5/2
Condition II: 8 × (x – 5/2)
Condition III: 8 × (x – 5/2) = 3x
⇒ 8x – 5/2 × 8 = 3x (Solving the bracket)
⇒ 8x – 20 = 3x
⇒ 8x – 3x = 20 (Transposing 3x to LHS and 20 to RHS)
⇒ 5x = 20
⇒ x = 20 ÷ 5 = 4 (Transposing 5 to RHS)
Thus, x = 4 is the required number.

Q4 : A positive number is 5 times another number. If 21 is added to both the numbers, then one of the new numbers becomes twice the other number. What are the numbers?
Solution:
Let the positive number be x.
Other number = 5x
Condition I: x + 21 and 5x + 21
Condition II: 5x + 21 = 2 (x + 21)
⇒ 5x + 21 = 2x + 42 (Solving the bracket)
⇒ 5x – 2x = 42 – 21 (Transposing 2x to LHS and 21 to RHS)
⇒ 3x = 21
⇒ x = 21 ÷ 3 = 7 (Transposing 3 to RHS)
Thus, the required numbers are 7 and 7 × 5 = 35.

Q5 : Sum of the digits of a two digit number is 9. When we interchange the digits, it is found that the resulting new number is greater than the original number by 27. What is the two-digit number?
Solution:
Let unit place digit be x.
Ten’s place digit = 9 – x
Original number = x + 10(9 – x)
Condition I: 10x + (9 – x) (Interchanging the digits)
Condition II: New number = original number + 27
⇒ 10x + (9 – x) = x + 10(9 – x) + 27
⇒ 10x + 9 – x = x + 90 – 10x + 27 (solving the brackets)
⇒ 9x + 9 = -9x + 117 (Transposing 9x to LHS and 9 to RHS)
⇒ 9x + 9x = 117 – 9
⇒ 18x = 108
⇒ x = 108 ÷ 18 (Transposing 18 to RHS)
⇒ x = 6

Unit place digit = 6
Ten’s place digit = 9 – 6 = 3
Thus, the required number = 6 + 3 × 10 = 6 + 30 = 36

Q7: One of the two digits of a two digit number is three times the other digit. If you interchange the digits of this two-digit number and add the resulting number to the original number, you get 88. What is the original number?
Solution:
Let unit place digit be x.
Ten’s place digit = 3x
Original number = x + 3x × 10 = x + 30x = 31x
Condition I: 10x + 3x = 13x (interchanging the digits)
Condition II: New number + original number = 88
13x + 31x = 88
⇒ 44x = 88
⇒ x = 88 ÷ 44 (Transposing 44 to RHS)
⇒ x = 2
Thus, the original number = 31x = 31 × 2 = 62
Hence the required number = 62

Q8 : mother’s present age is six times Shobo’s present age. Shobo’s age five years from now will be one third of his mother’s present age. What are their present ages?
Solution:
Let Shobo’s present age be x years.
Shobo’s mother’s age = 6x years.
After 5 years Shobo’s age will be (x + 5) years.
As per the condition, we have
x + 5 = 1/3 × 6x
⇒ x + 5 = 2x
⇒ 5 = 2x – x (Transposing x to RHS)
⇒ 5 = x
Hence Shobo’s present age = 5 years
and Shobo’s mother’s present age 6x = 6 × 5 = 30 years.

Q9 :There is a narrow rectangular plot, reserved for a school, in Mahuli village. The length and breadth of the plot are in the ratio 11 : 4. At the rate of ₹ 100 per metre, it will cost the village panchayat ₹ 75000 to fence the plot. What are the dimensions of the plot?
Solution:
Let the length and breadth of the plot be 11x m and 4x m respectively.
Fencing all around = perimeter of the rectangular plot
Perimeter of the plot = 75000/100 = 750 m
2(l + b) = 750
⇒ 2(11x + 4x) = 750
⇒ 2(15x) = 750
⇒ 30x = 750
⇒ x = 750 ÷ 30 = 25
length = 11 × 25 m = 275 m
and breadth = 4 × 25 m = 100 m

Q10 :A grandfather is ten times older than his granddaughter. He is also 54 years older than her. Find their present ages.
Solution:
Let the present age of granddaughter = x years.
the present age of grandfather = 10x years.
As per the conditions, we have
10x – x = 54
⇒ 9x = 54
⇒ x = 54 ÷ 9 = 6 [Transposing 9 to RHS]
Hence, the present age of the granddaughter = 6 years
and the present age of grandfather = 6 × 10 = 60 years.

Q11 :Aman’s age is three times his son’s age. Ten years ago he was five times his son’s age. Find their present ages.
Solution:
Let the present age of the son be x years.
Present age of Aman = 3x years
10 years ago, the son’s age was = (x – 10) years
10 years ago, the father’s age was = (3x – 10) years
As per the conditions, we have
5(x – 10) = 3x – 10
⇒ 5x – 50 = 3x – 10
⇒ 5x – 3x = 50 – 10(Transposing 3x to LHS and 50 to RHS)
⇒ 2x = 40
⇒ x = 40 ÷ 2 = 20
Hence, the son’s age = 20 years.
and the age of Aman = 20 × 3 = 60 years.

Q12 :

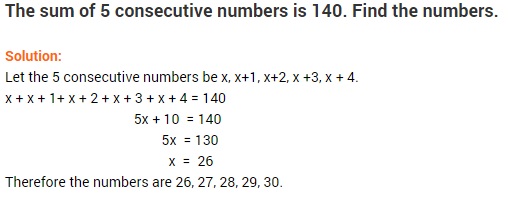
Q14 :

Q15 :

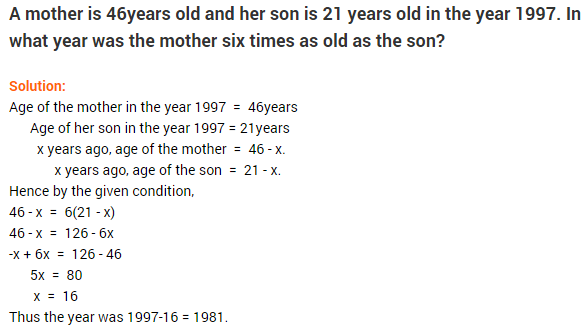
Q16 :The difference between two whole numbers is 66. The ratio of the two numbers is 2 : 5. What are the two numbers?

Solution: Let the two whole numbers be 2x and 5x . The difference between 2x and 5x is 66. So,

5x-2x=66

3x=66

x=66/3

x=22

Therefore the two numbers are

5x=5*22=110

2x=2*22=44

Q17: The ratio of two numbers is 3:4. If 12 is added to each of the two numbers, the ratio becomes 5:6. What is the sum of the two numbers?

Solution:

Let the two numbers be 3x and 4x. (Don’t take x and y here as ratio is given)

As per the question,

3x+12 : 4x+12 = 5:6

Now by cross multiplication

(3x+12)(6) = (4x+12)(5)

which gives → 18x+72 = 20x+60 → 72–60 = 20x-18x → 2x=12 → x=6

So the numbers are 3x and 4x which are 3 x 6 and 4 x 6 = 18 and 24.

Q18:Two numbers are in the ratio 5:3. If they differ by 18, what are the numbers?

Solution:

Let the two numbers be 5x, 3x.

5x-3x = 18

2x = 18

Divide LHS and RHS by 2.

2x/2 = 18/2

x = 9

5x= 5x9 = 45

3x= 3x9 = 27

27, 45 : Final Answer

Q19:Two numbers are in the ratio 3:5. If 8 is added to both the numbers, the ratio becomes 2:3. What is the larger number?

Solution:

Let the numbers be 3x and 5x

(3x+8):(5x+8) = 2:3, or

3(3x+8) = 2(5x+8), or

9x+24 = 10x+16, or

10x-9x = x = 24–16=8

The numbers of the first ratio are 24 and 40. Here the larger number is 40.

And, the numbers of the second ratio are 32 and 48. Thus the larger number is 48.

Q20:Two numbers are in the ratio 3. ratio 5 is increased by 10. The ratio between the new number is 5 ratio 7. What is the original number?

Solution:

Let the two numbers be x and y.

$\frac{x}{y} = \frac{3}{5}$

$\frac{x + 10}{y + 10} = \frac{5}{7} ⟹ 7 x + 20 = 5 y$

soling these two equations, we get $x = 15, y = 25.$

Q21:Two numbers are in the ratio 2:5. If they differ by 18, what are the corresponding numbers?

Solution:

THE NUMBERS ARE SUPPOSE 2X AND 5 X. DIFFERENCE IS 3X.

3 X = 18. X = 6.

THE NUMBERS ARE 12 AND 30. DIFFERENCE 🙂 18

Q22:Two years ago, Dilip was three times as old as his son and two years hence , twice his age will be equal to five times that of his son. Find their present ages.

Solution:

Let Dilip's son's age 2 years ago be x years. Then, Dilip's age 2 years ago = (3x) years.

.·. the son's age 2 years hence = ( x + 4 ) years.

Dilip's age 2 years hence = ( 3x + 4 ) years.

.·. 2 ( 3x + 4 ) = 5 ( x + 4 )

=> 6x + 8 = 5x + 20

=> 6x - 5x = 20 - 8

=> x = 12.

.·. Dilip's son's age 2 years ago = 12 years.

And Dilip's age 2 years ago = 3 × 12 = 36 years.

.·. son's present age = 14 years, and

Dilip's present age